1. Vecteurs dans le plan
Notion de vecteur
Dans le cours Nous avons vu dans un chapitre précédent la notion de vecteur.
Un vecteur est défini par la donnée d’une direction, un sens et une longueur (qu’on appelle aussi la norme du vecteur).
Soit $A$ et $B$ deux points du plan, alors le vecteur $\overrightarrow{AB}$ a pour direction la droite $(AB)$, pour sens le sens qui va de $A$ vers $B$ et pour norme la longueur $AB$.
Nous avons également défini les trois opérations sur les vecteurs, à savoir comment calculer la somme ou la différence de deux vecteurs par la relation de Chasles et la règle du parallélogramme. Nous avons aussi défini le produit d’un vecteur par un réel comme agrandissement, ou réduction ou changement de sens.
Dans ce cadre, on rappelle que deux vecteurs $\vec u$ et $\vec v$ sont colinéaires s’ils ont la même
direction. Autrement dit, s’il existe un réel $k$ tel que : $\boxed{~~v=k\vec u~~}$ ou, ce qui revient au même, s’il existe un réel $k’$ tel que : $\boxed{~~u=k’\vec v~~}$
2. Caractérisation d’une droite. Repère et graduation de la droite
Théorème 1 et définition.
Soit $O$ un point quelconque du plan et $\vec u$ un vecteur non nul. Alors l’ensemble des points $M$ du plan tels que $\overrightarrow{OM}$ est colinéaire à $\vec u$ définit la droite $d$ passant par $O$ et ayant pour direction le vecteur $\vec u$.
Autrement dit : $$M\in d\quad\text{si, et seulement si, }[\text{il existe un réel }x\text{ tel que } \overrightarrow{OM}=x\vec u]$$ $x$ s’appelle l’abscisse de $M$ et se note $x_M$ dans la graduation $(O;\vec u)$, ou dans le repère $(O;\vec u)$ de la droite graduée $d$.
Remarque
Deux vecteurs colinéaires ont la même direction. Donc, ils définissent la même droite passant par un point $O$ donné.
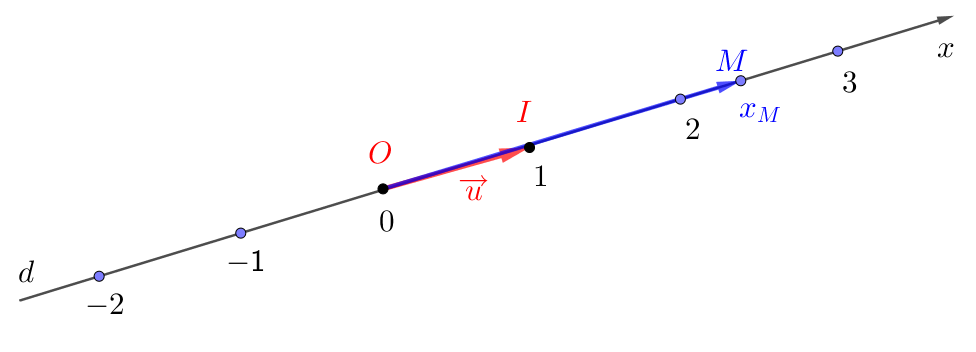
c’est-à-dire $\overrightarrow{OI}=\vec u$ et $OI=1$.
Définition 1.
Le couple $(A,\vec u)$ forme une graduation ou un repère de la droite $d$. $O$ est l’origine de la graduation et $I$= le point unité, c’est-à-dire $\overrightarrow{OI}=\vec u$.
On dit que le vecteur $\vec u$ est un vecteur directeur de la droite $d$.
On dit aussi que le vecteur $\vec u$ est un vecteur de base, ou forme une base de l’ensemble des vecteurs de la droite $d$.
3. Caractérisation d’un plan : Base de l’ensemble des vecteurs du plan
D’une manière analogue, si $O$ est un point du plan et $\vec\imath$ et $\vec\jmath$ sont deux
vecteurs non colinéaires du plan, alors le triplet $(O;\vec\imath,\vec\jmath)$ définit un repère du plan
$(O;I,J)$, où $O$, $I$ et $J$ sont les points non alignés tels que $\overrightarrow{OI}=\vec\imath$ et $\overrightarrow{OJ}=\vec\jmath$.
Définition 2.
Soient $\vec u$ et $\vec v$ deux vecteurs non nuls du plan. On dit que $\vec u$ et $\vec v$ sont des vecteurs de base ou que le couple de vecteurs $(\vec u;\vec v)$ forme une base de l’ensemble des vecteurs du plan, lorsque les deux vecteurs $\vec u$ et $\vec v$ sont non nuls et non colinéaires.
Caractérisation d’un plan :
Soit $M$ un point quelconque. Alors $M$ appartient au plan $(O;I,J)$ si, et seulement si, le vecteur $\overrightarrow{OM}$ s’exprime comme « combinaison linéaire » des deux vecteurs de base $\vec\imath$ et $\vec\jmath$.
Théorème 2.
Soit $O$ un point quelconque du plan et $\vec\imath$ et $\vec\jmath$ deux vecteur non nuls et non colinéaires qui forment une base de l’ensemble des vecteurs du plan. Alors :
Pour tout vecteur $\overrightarrow{V}$ du plan, il existe un unique couple $(x;y)$ de nombres réels tels que : $$\boxed{~~\overrightarrow{V}=x\vec\imath+y\vec\jmath~~}$$ Le couple $(x;y)$ forme les coordonnées du vecteur $\overrightarrow{V}$
Notation.
Les coordonnées d’un point $M$ du plan se notent en ligne. Les coordonnées d’un vecteur se notent en colonne comme ceci : Les coordonnées du vecteur $\overrightarrow{V}$ se notent de la manière suivante : $$\boxed{~~\overrightarrow{V}\dbinom{x}{y}~~}$$ $x$ est l’abscisse du vecteur $\overrightarrow{V}$ et $y$ est l’ordonnée du vecteur $\overrightarrow{V}$.
Démonstration
Soit $M$ un point du plan. On décompose le vecteur $\overrightarrow{OM}$ avec la règle du parallélogramme. Par construction $OAMB$ est un parallélogramme.
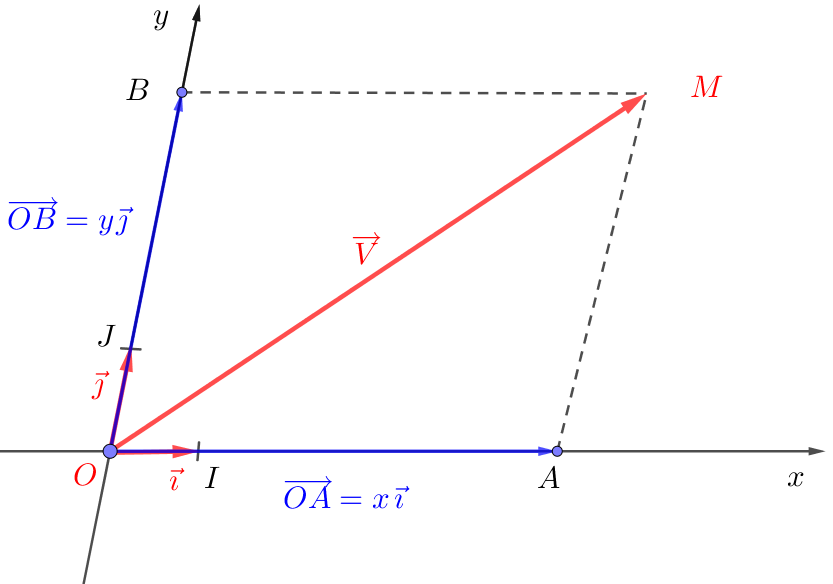
D’après la règle du parallélogramme, on a bien : $$\overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{OB}$$ Or le vecteur $\overrightarrow{OA}$ est colinéaire à $\vec\imath=\overrightarrow{OI}$. Donc, il existe un nombre réel $x$ tel que : $\overrightarrow{OA}=x\overrightarrow{OI}$. Ce qui donne : $$\overrightarrow{OA}=x\vec\imath$$
D’une manière analogue, le vecteur $\overrightarrow{OB}$ est colinéaire à $\vec\jmath$. Donc, il existe un nombre réel $y$ tel que : $\overrightarrow{OB}=y\overrightarrow{OI}$. Ce qui donne : $$\overrightarrow{OB}=y\vec\imath$$
Par conséquent, $$\begin{array}{rcl}\overrightarrow{OM}&=&\overrightarrow{OA}+\overrightarrow{OB}\\
&=&x\overrightarrow{OI}+y\overrightarrow{OJ}\\ &=&x\vec\imath+y\vec\jmath\\ \end{array}$$
Conclusion. Pour tout vecteur $\overrightarrow{V}$ du plan, il existe un unique couple $(x;y)$ de nombres réels tels que : $$\boxed{~~\overrightarrow{V}=x\vec\imath+y\vec\jmath~~}$$
Remarque
Nous avons vu dans le chapitre sur le repérage dans le plan différents types de repères du plan.
Le repère est quelconque si on ne précise aucune condition.
Le repère est orthogonal si, et seulement si, les deux axes sont perpendiculaires : $(OI)\perp(OJ)$.
Le repère est normé si, et seulement si, les deux segment unité sont de même longueur égale à $1$ : $OI=OJ$.
Le repère est orthonormé ou orthonormal si, et seulement si, le repère est à la fois orthogonal et normé.
4. Coordonnées d’un point dans le plan
Théorème 3.
Soit $O$ un point quelconque du plan et $\vec\imath$ et $\vec\jmath$ qui forment une base de l’ensemble des vecteurs du plan. Alors :
Pour tout point $M$ du plan, il existe un couple $(x;y)$ de nombres réels tels que : $$\boxed{~~\overrightarrow{OM}=x\vec\imath+y\vec\jmath~~}$$ Le couple $(x;y)$ forme les coordonnées du vecteur $\overrightarrow{OM}$ et se notent : $(x_M;y_M)$.
Les coordonnées du point $M$ sont notées $(x_M;y_M)$ [en ligne], $x_M$ est l’abscisse de $M$ et $y_M$ est l’ordonnée de $M$.
5. Exercices résolus
v
Exercice 1. Dans le repère $(O;\vec\imath,\vec\jmath)$ de la figure ci-dessous, déterminer par lecture graphique, les coordonnées des vecteurs donnés.
A TERMINER
Exercice 2. Dans le repère $(O;\vec\imath,\vec\jmath)$, placer les vecteurs suivants dans le plan, localisés aux points de votre choix.
