Suites géométriques. Relation de récurrence. Forme explicite

Les suites géométriques jouent un rôle important en mathématiques comme modèles discrets d’évolutions constantes à croissance exponentielle. D’autres part, ce sont des suites qui s’expriment sous une forme récurrente et sous une forme explicite.

Sommaire

1. Suites géométriques définies par récurrence. Exemple.
2. Comment démontrer qu’une suite est géométrique ? Exemple.
3. Définition explicite d’une suite géométrique. Exemple.
4. Existe-t-il une fonction associée à une suite géométrique ?

---

1. Suites géométriques définies par récurrence

Définition 1.
Soit $q$ un nombre réel strictement positif. On dit qu’une suite $(v_n)$ est une suite géométrique de raison $q$, lorsqu’on donne un premier terme $v_0$ et chaque terme s’obtient en multipliant le terme précédent par $q$.
Autrement dit : la suite $(v_n)$ est définie pour tout entier $n\geqslant0$ par : $$\left\{\begin{array}{l} v_0\in\R\text{ est donné}\\ v_{n+1}=q\times v_n\\ \end{array}\right.$$ $v_n$ s’appelle le terme général de la suite.
La raison $q$ peut être assimilée à un coefficient multiplicateur d’un terme au terme suivant.

Illustration : $$v_0\, {\color{brown}{—\boxed{\times q}\!\!\rightarrow}} v_1\, {\color{brown}{—\boxed{\times q}\!\!\rightarrow}} v_2\, {\color{brown}{—\boxed{\times q}\!\!\rightarrow}} v_3~\cdots v_n\, {\color{brown}{—\boxed{\times q}\!\!\rightarrow}} v_{n+1}$$

Si la suite commence au rang $1$, on commence à partir de $v_1$.

Exemple 1.
1°) Déterminer la nature de la suite définie pour tout entier $n\geqslant0$ par $$\left\{ \begin{array}{l}v_0=2 ; \\ v_{n+1}=v_n\times 0,5\\ \end{array}\right.$$ 2°) Calculer les quatre premiers termes de la suite $(v_n)$.

---

2. Comment démontrer qu’une suite est géométrique ?

Propriété 1.
1°) Pour démontrer qu’une suite est géométrique, il faut démontrer qu’il existe un réel $q\not=0$ tel que pour tout entier naturel $n$ : $$\color{brown}{\boxed{~v_{n+1}=q\times v_n~}}$$
2°) Pour démontrer qu’une suite est géométrique, il suffit de montrer que pour tout entier naturel $n$, $v_n\not=0$ et le quotient $\dfrac{v_{n+1}}{v_n}=q$ est une constante (indépendante de $n$).
Cette constante $q$ est la raison de la suite géométrique.

Exercice 2.
Soit $(v_n)$ la suite définie pour tout entier $n$ par : $v_n=3\times 2^n$.
1°) Démontrer que la suite $(v_n)$ est géométrique.
2°) Déterminer ses éléments caractéristiques.

---

3. Définition explicite d’une suite géométrique

Théorème 1.
Soit $(v_n)$ une suite géométrique de raison $q\in\R^{+*}$.
$\bullet$ Si le premier terme est $v_0$, alors le terme général $v_n$ de la suite est donné par pour tout entier $n\geqslant0$ : $$\boxed{\;v_{n}=v_0\times q^n \;}$$
$\bullet$ Si le premier terme est $v_1$, alors le terme général $v_n$ de la suite est donné par pour tout entier $n\geqslant1$ : $$\boxed{\;v_{n}=v_1\times q^{n-1} \;}$$
$\bullet$ Si le premier terme est $v_2$, alors le terme général $v_n$ de la suite est donné par pour tout entier $n\geqslant2$ : $$\boxed{\;v_{n}=v_2\times q^{n-2} \;}$$ Et ainsi de suite.

Avec l’expression explicite, on peut calculer le terme de n’importe quel rang $n$.

Exemple 3.
On considère la suite définie pour tout entier $n\geqslant0$ par $$\left\{ \begin{array}{l}v_0=10 ; \\ v_{n+1}=2\times v_n\\ \end{array}\right.$$ 1°) Donner l’expression explicite de la suite $(v_n)$.
2°) Calculer $v_{1}$, $v_2$ et $v_{10}$.

---

4. Existe-t-il une fonction associée à une suite géométrique ?

Eh bien, la réponse est : OUI. C’est une fonction exponentielle.

Exemple.
Soit $(v_n)$ la suite géométrique de raison $q=1,5\in\R^{+*}$ et de premier terme $v_0=1$.
On sait calculer $(1,5)^n$ pour tout entier naturel $n$ et même pour tout entier négatif $-n$, avec la formule sur les puissances vues en 4ème : $q^{-n}=\dfrac{1}{q^n}$.

Ceci permet de définir sur $\R$ une nouvelle fonction $f: x\mapsto f(x)= q^x$. Dans cette fonction, définie sur tout $\R$, la variable est située dans l’exposant. On aurait pu l’appeler « fonction exposantielle », mais comme en anglais un exposant se dit « exponent », les fonctions du type $f:x\mapsto f(x)= q^x$, $q>0$ et $q\not=1$, s’appellent des « fonctions exponentielles ».

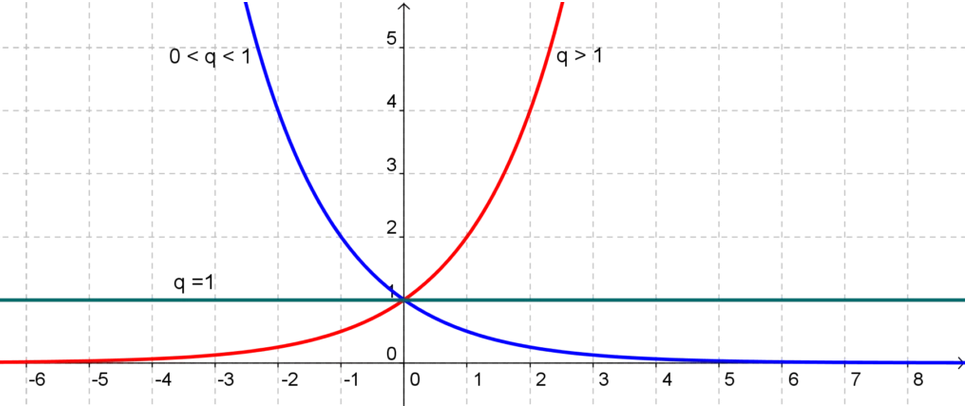
• Si $q>1$, la fonction $f:x\mapsto f(x)= q^x$. $f$ est strictement croissante sur (tout) $\R$.
• Si $0<q<1$, la fonction $f:x\mapsto f(x)=q^x$. $f$ strictement décroissante sur (tout) $\R$.
• Si $q=1$, $1^x=1$, donc a fonction $f:x\mapsto f(x)=1^x=1$ est la fonction constante et égale à 1, représentée graphiquement par la droite parallèle à l’axe des abscisses, d’équation $y=1$.

Représentations graphiques suivant les 3 cas. Ce qui nous donnera l’allure des courbes des suites géométriques dans ces trois cas.

Ces fonctions conservent les mêmes propriétés calculatoires que les « puissances » vues en classe de 4ème. Entre autres : $q^{x+y}=q^x\times q^x$. Ce qui nous facilite la tâche.

Exemple
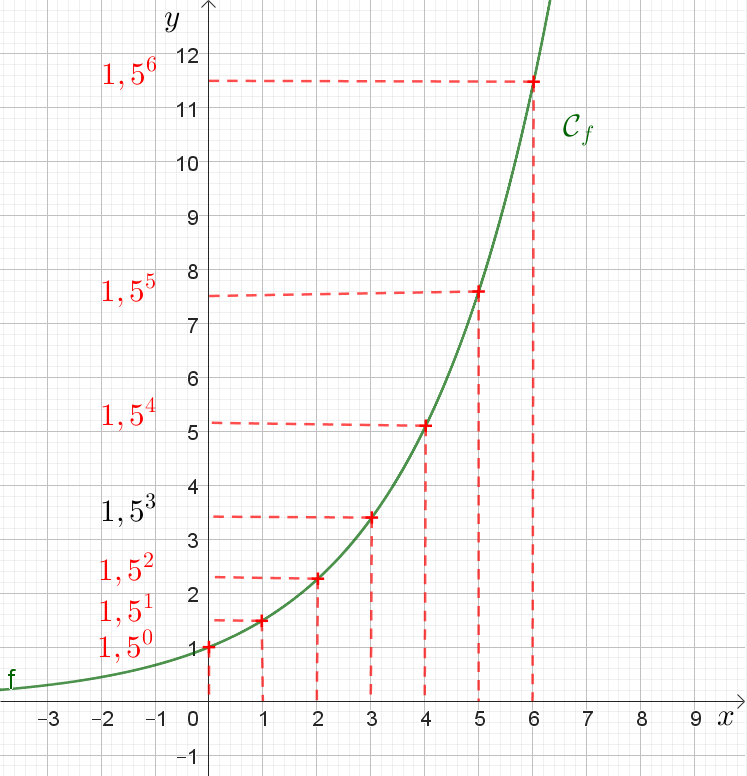
On peut donc définir la fonction $f$ sur $\R$ par $f(x)=1,5$

Exemple 4.
On peut donc définir la fonction $f$ sur $\R$ par $f(x)=1,5^x$ et la suite $(v_n)$ définie par : $v_n=1,5^n$.
1°) Construire avec Geogebra ou sur votre calculatrice, la représentation graphique de la fonction $f$.
2°) Placer sur le même graphique les points $A_n=(n;v_n)$ représentant la suite $(v_n)$.

---

Exemple 5.
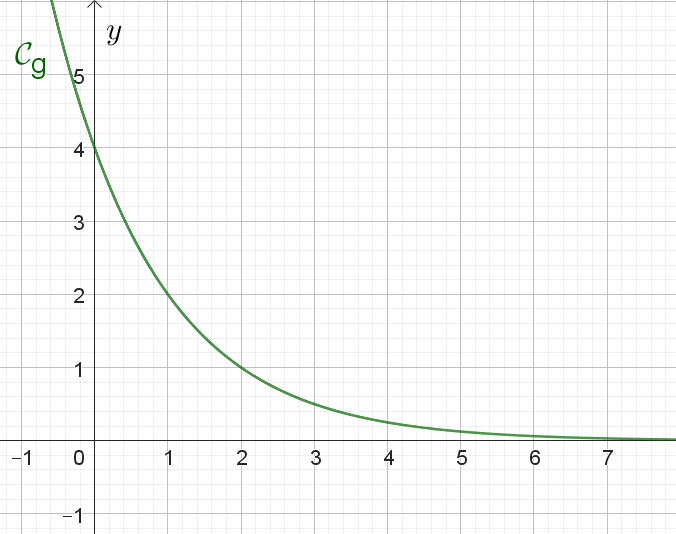
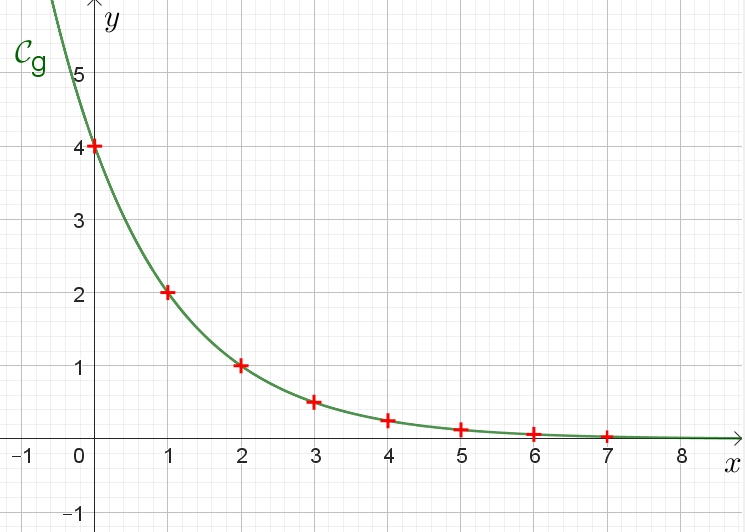
On considère la suite géométrique $(v_n)$ de premier terme $v_0=4$ et pour tout entier naturel $n$ : $v_{n+1}=\dfrac{1}{2}v_n$.
1°) Déterminer l’expression explicite de la suite $(v_n)$.
En déduire l’expression de la fonction $g$ associée à cette suite $(v_n)$ et construire avec Geogebra ou sur votre calculatrice, la représentation graphique de la fonction $g$.
2° a) Donner le sens de variation de la fonction $g$.
b) En déduire le sens de variation de la suite $(v_n)$.
3°) Placer sur le même graphique les points $A_n=(n;v_n)$ représentant la suite $(v_n)$.

---

x