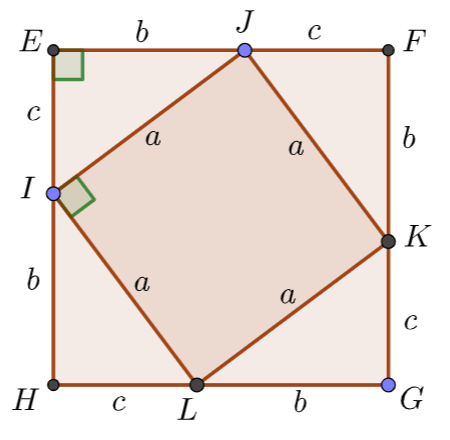
Lorsqu’on connaît trois informations dans un triangle, on peut tout calculer, les longueurs des côtés, les mesures des angles, le périmètre et l’aire du rectangle. Dans un triangle rectangle, nous savons déjà qu’il y a un angle droit. Si on connaît en plus les longueurs de deux côtés, on sait calculer le troisième côté et , en utilisant la trigonométrie, on sait calculer les mesures des angles aigus. Nous avons besoin, dans ce chapitre de la notion de racine carrée d’un nombre positif.

1. Racine carrée d’un nombre positif

Consulter la page « Découverte de la racine carrée d’un nombre réel positif » pour démarrer.

Si on connaît un nombre $c$, on peut calculer son carré $c^2=c\times c$, par un calcul direct ou en utilisant la calculatrice avec la touche $\boxed{~x^2~}$.

Inversement, Si on connaît la carré $c^2$ d’un nombre $c$, peut-on calculer la valeur exacte ou simplement une valeur approchée de $c$ ?
Par exemple, si on connaît l’aire d’un carré $a=20~$cm${}^2$, peut-on connaître la longueur du côté $c$ du carré ?
La réponse est « OUI ». Comment ?

$\bullet$ Bien sûr, si $a=25$, c’est un « carré parfait ». On sait que $25=5^2$, on pourrait dire : $c=5$.
C’est bon, mais c’est insuffisant car $c=-5$ est aussi solution. On aura donc deux solutions $5$ et $-5$.
Il faut donc préciser que « $c$ est une longueur, donc : $c>0$ » pour conclure que $c=5$.

$\bullet$ Si $a=20$, ce n’est pas un « carré parfait ». il est plus difficile de trouver à la main, la valeur exacte. A la calculatrice, on utilise la touche : $\boxed{~\sqrt{.}~}$ (écran limité à 10 chiffres). On obtient un nombre à 9 décimales : $c=\sqrt{20} = 4,472135955\ldots$ qui ne s’arrête pas.
Ce n’est pas une valeur exacte. On peut trouver une valeur approchée arrondie à $10^{-1}$ ou à $10^{-2}$ près. On pourrait conclure que : $$\boxed{c=\sqrt{20}\simeq 4,47~\text{cm}~}$$

$\bullet$ Si $a=2,25$, on obtient à la calculatrice : $c=\sqrt{2,25}=1,5$ qui est une valeur exacte car $1,5^2=2,25$.

Haut de page

2. Le théorème de Pythagore dans le triangle rectangle

2.1. Description d’un triangle rectangle

Soit $ABC$ un triangle rectangle en $A$.
Le côté opposé à l’angle droit est le côté le plus long s’appelle l’hypoténuse.
Les deux autres côtés $[AB]$ et $[AC]$ s’appellent « Les côtés de l’angle droit ».

2.2. Énoncé du théorème de Pythagore

Théorème de Pythagore.
Si un triangle est rectangle, alors la carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux côtés qui forment l’angle droit.

Soit $ABC$ est un triangle rectangle en $A$ tel que $AB=c$ et $AC=b$ et $BC=a$.
On construit un « grand carré » $EFGH$ de côté $b+c$, avec 4 copies du triangle $ABC$ comme indiqué dans la figure suivante.

Démonstration du théorème de Pythagore

Dans un triangle rectangle, les deux angles aigus sont complémentaires.
Donc, on a : $\widehat{EIJ}+\widehat{EJI}=90^\circ$. Donc $\widehat{EIJ}+\widehat{HIL}=90^\circ$. On en déduit que : $\widehat{JIL}=90^\circ$.
De même pour les autres angles.
Le quadrilatère $IJKL$ est donc un carré.
On calcule l’aire du grand carré $EFGH$ de deux manières :
D’une part : $$\begin{array}{l} {\mathcal A} =EF^2\\
{\mathcal A} =(b+c)^2\\
\boxed{~{\mathcal A} =b^2+2bc+c^2~}\quad(1)\\
\end{array}$$ Et D’autre part : $$\begin{array}{l} {\mathcal A} =\text{aire}(IJKL)+4\times\text{aire}(EIJ)\\
{\mathcal A} =a^2+4\times\dfrac{bc}{2}\\
\boxed{~{\mathcal A} =a^2+2bc~}\quad(2)\\
\end{array}$$ En identifiant les deux écritures de l’aire (1) et (2), on obtient : $$a^2+2bc=b^2+2bc+c^2$$ Finalement, en éliminant le terme $2bc$ des deux côtés, on obtient : $$\boxed{~a^2=b^2+c^2~}$$
CQFD.$\blacktriangle$

Haut de page

3. Illustration géométrique du théorème de Pythagore

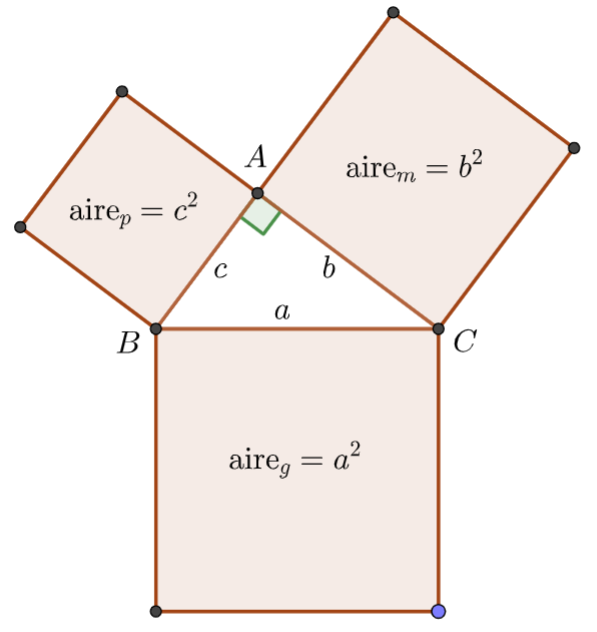
On peut traduire donc le théorème de Pythagore par « Dans un triangle rectangle, l’aire du carré construit sur l’hypoténuse est égal à la somme des aires des deux carrés construits sur les deux autres côtés ». On peut l’illustrer par le principe du Sablier aux trois carrés :

Principe du Sablier. Illustration du Théorème de Pythagore
Principe du Sablier. Illustration du Théorème de Pythagore

4. Exercices résolus

Exercice résolu n°1.
Soit $ABC$ un triangle rectangle en $A$ tel que $AB=3~$cm et $AC=4~$cm.
Calculer la valeur exacte de $BC$.

On sait que le triangle $ABC$ est rectangle en $A$. Son hypoténuse est $[BC]$.
Donc d’après le théorème de Pythagore, on a : $$\begin{array}{rl}BC^2&=AB^2+AC^2\\ &=3^2+4^2\\ &=9+16 \\ BC^2 &=25 \\
\end{array}$$ Or $BC$ est une longueur. Donc $BC>0$. Donc $BC=\sqrt{25}$.
Par conséquent : $\boxed{~BC=5~}$. CQFD.$\blacktriangle$
Ici, nous n’avons pas besoin de calculatrice, car $5^2=25$ donc $\sqrt{25}=5$.

Exercice résolu n°2.
On considère un triangle $RST$ rectangle en $R$ tel que $RS=4~$cm et $ST=8~$cm.
Calculer la valeur exacte de $RT$ puis en donner une valeur approchée arrondie au centième près.

On sait que le triangle $RST$ est rectangle en $R$. Son hypoténuse est $[ST]$.
Donc d’après le théorème de Pythagore, on a : $$\begin{array}{rl}RT^2+RS^2&=ST^2\\
RT^2+4^2&=8^2\\ RT^2+16&=64 \\ RT^2 &=64-16 \\ RT^2&=48\\
\end{array}$$ Or $RT$ est une longueur. Donc $RT>0$. Donc $RT=\sqrt{48}$.
Par conséquent, la valeur exacte de $RT$ est :$$\boxed{~RT=\sqrt{48}~}$$
A la calculatrice, on obtient : $\sqrt{48}=6,92820323\ldots$.
Une valeur approché au centième près est donc : $$\boxed{~RT\simeq6,93~\text{cm}~}$$
CQFD.$\blacktriangle$

Exercice résolu n°3.
Soit $IJK$ un triangle rectangle en $J$ tel que $IK=12~$cm et $IJ=8~$cm.
Calculer la valeur exacte de $JK$ puis en donner une valeur approchée arrondie au centième près.

A terminer
CQFD.$\blacktriangle$

Haut de page