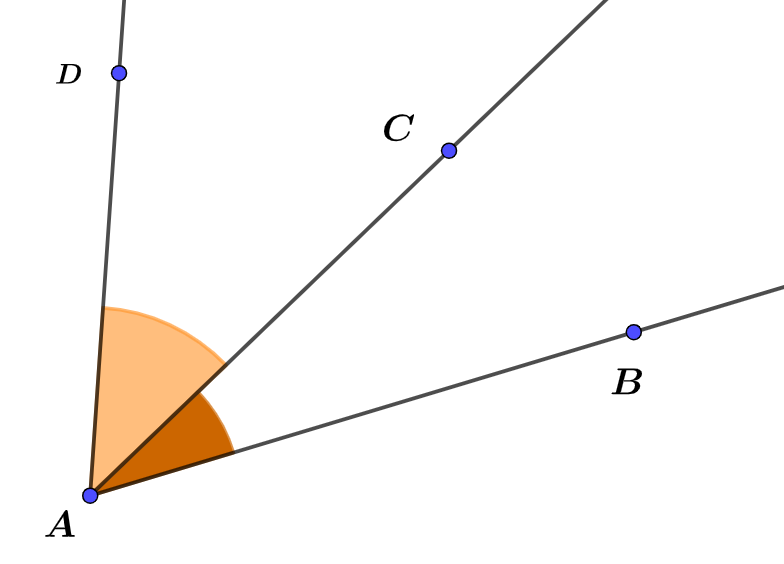
Dans cette page, nous donnons les définitions des différents types angles que nous rencontrons en géométrie au Collège.

1. C’est quoi un angle ?

Définition 1.
Un angle, noté $\widehat{xOy}$ est formé par deux demi-droites $[Ox)$ et $[Oy)$ de même origine $O$.
$\bullet$ Le point $O$ s’appelle le sommet de l’angle.
$\bullet$ Les deux demi-droites $(Ox)$ et $(Oy)$ s’apellent les côtés de l’angle $\widehat{xOy}$.

Notations :
$\widehat{xOy}$ = l’angle de sommet $O$ et de côtés les demi-droites $[Ox)$ et $[Oy)$.
$\widehat{BAC}$ = l’angle de sommet $A$ et de côtés les demi-droites $[AB)$ et $[AC)$.

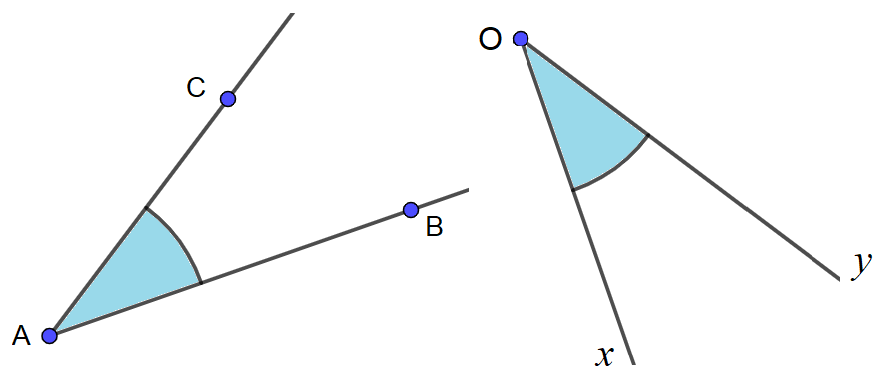
Vocabulaire des angles aigus

Figure 1.
Les angles $\widehat{BAC}$ et $\widehat{xOy}$

2. Unité de mesure d’un angle

Définition 2.
L’unité de mesure des angles est le degré, noté par un petit rond. par exemple « 90° » se lit « 90 degrés ».
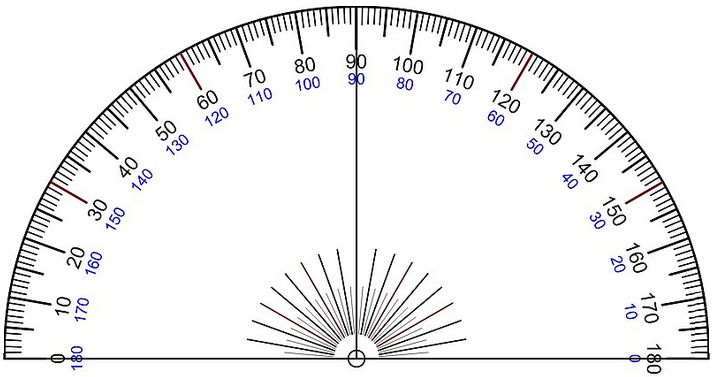
L’instrument de mesure des angles est le rapporteur. (Attention à la position du centre !)

Vocabulaire des angles rapporteur
Figure 2.

3. Angles particuliers

Définition 3.
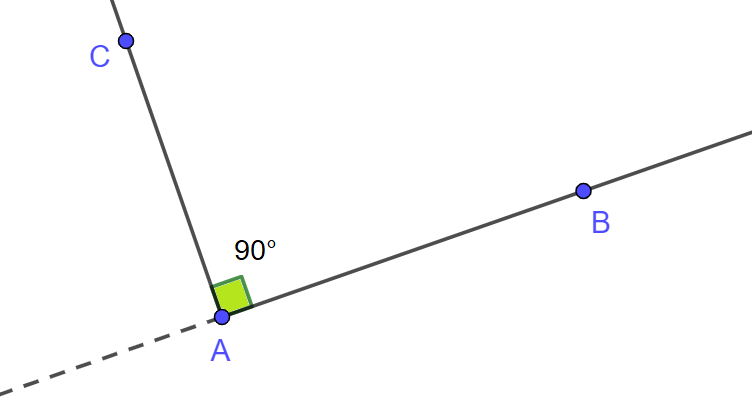
Deux demi-droites perpendiculaires forment un angle droit $$\boxed{~\widehat{BAC}=90^\circ~}$$ Un angle droit correspond à un quart de tour autour de $A$.

Figure 3.

Définition 4.
Deux demi-droites opposées forment une droite, donc un angle plat $$\boxed{~\widehat{xAy}=180^\circ=\widehat{BAC}~}$$ Un angle plat correspond à un demi-tour autour de $A$.

Figure 4.

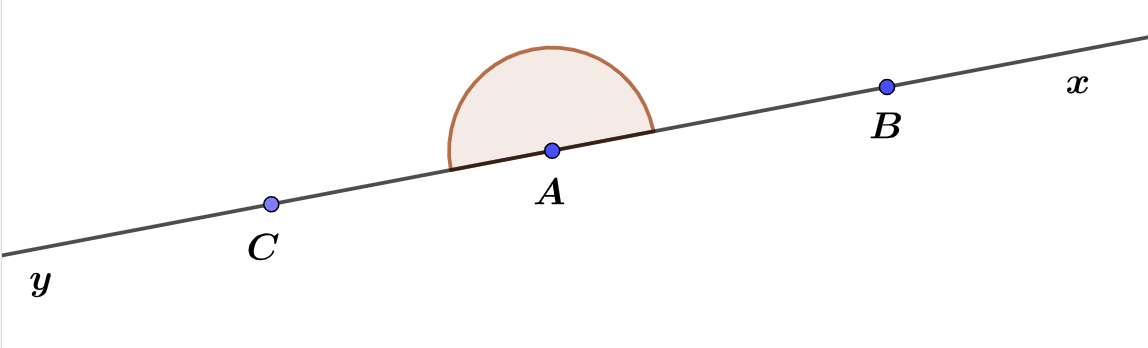
Définition 5.
Un angle aigu est un angle plus petit que l’angle droit : $$\boxed{~\widehat{xOy}<90^\circ~}$$

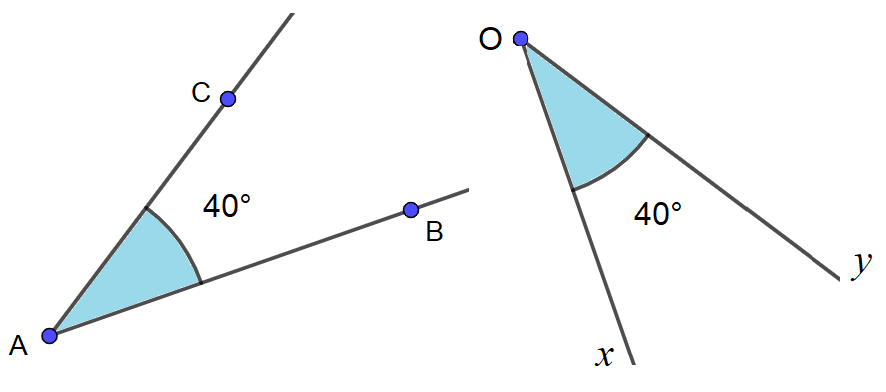
Exemples.
Les angles de la figure 1, sont tous les deux des angles aigus. Ils mesurent chacun 40°.

Vocabulaire des angles aigus
Figure 5.

Définition 6.
Un angle obtus est un angle plus grand qu’un angle droit et plus petit qu’un angle plat : $$\boxed{~90^\circ<\widehat{ABC}<180^\circ~}$$

Vocabulaire des angles obtus
Figure 6.

Définition 7.
Un angle saillant est un angle $\widehat{xOy}$ plus petit qu’un angle plat : $$\boxed{~\widehat{xOy}<180^\circ~}$$

Exemples.
Les angles aigus et obtus sont des angles saillants.

Définition 7.
Un angle rentrant est un angle $\widehat{xOy}$ plus grand qu’un angle plat : $$\boxed{~180^\circ<\widehat{xOy}<360^\circ~}$$

Définition 8.
L’angle nul est un angle saillant dont les deux côtés sont superposés : $$\boxed{~\widehat{xAx}=0^\circ=\widehat{BAB}~}$$

Figure 7. Angle nul

Définition 9.
L’angle plein est un angle rentrant dont les deux côtés sont superposés : $$\boxed{~\widehat{xAx}=360^\circ=\widehat{BAB}~}$$

Figure 8. Angle plein

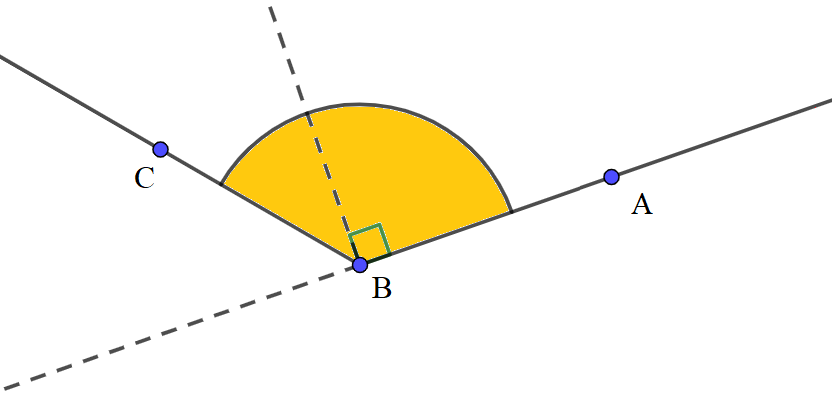
Définition 10.
Deux angles $\widehat{a}$ et $\widehat{b}$ sont dits complémentaires lorsque, en les juxtaposant, on obtient un angle droit. Autrement dit : Deux angles sont complémentaires si la somme de leurs mesures est égale à $90^\circ$ : $$\boxed{~\widehat{a}+\widehat{b}=90^\circ~}$$

Figure 9.

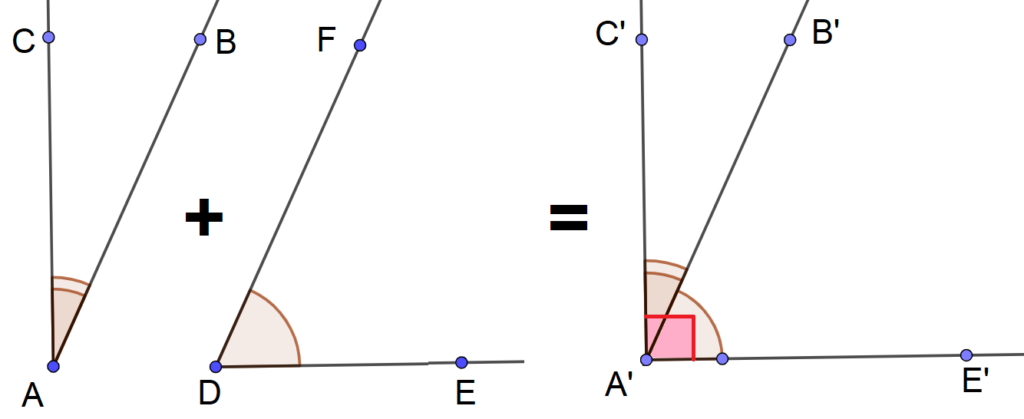
Exemple : $35^\circ$ et $55^\circ$ sont complémentaires.

Définition 11.
Deux angles $\widehat{a}$ et $\widehat{b}$ sont dits supplémentaires lorsque, en les juxtaposant, on obtient un angle plat. Autrement dit : Deux angles $\widehat{a}$ et $\widehat{b}$ sont dits supplémentaires si la somme de leurs mesures est égale à $180^\circ$ : $$\boxed{~\widehat{a}+\widehat{b}=180^\circ~}$$

Figure 10.
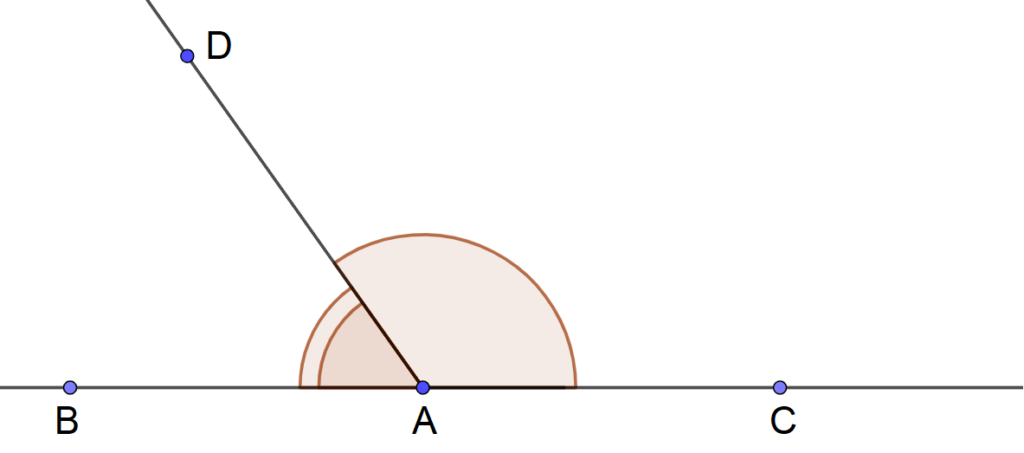
$\widehat{BAD}+\widehat{CAD}=180°$

Exemple : $115^\circ$ et $65^\circ$ sont supplémentaires.

Définition 12.
Deux angles sont dits adjacents si les trois conditions suivantes sont vérifiées :
1°) Les deux angles ont le même sommet $O$ ;
2°) Ils ont un côté commun ;
3°) Et ils sont situés de part et d’autre de ce côté commun.

« de part et d’autre » = « de chaque côté » = « d’un côté et de l’autre côté ». Exemple : « La ville s’étend de part et d’autre du fleuve » = « La ville s’étend d’un côté et de l’autre côté du fleuve ».

Figure 11.