L’idée de base est de représenter toutes les options possibles de la situation sous forme d’un arbre où chaque nœud représente une décision ou un état. Les branches représentent les différentes possibilités à chaque étape. Les feuilles de l’arbre représentent les résultats finaux ou les issues possibles.
La construction d’un schéma en arbre permet de distinguer tous les cas possibles, donc toutes les issues possibles. La racine $\Omega$ correspond au premier « noeud ». Les branches sont représentées par des flèches pour énumérer tous les cas possibles. Une branche = Un cas.
Puis on recommence, à partir de chaque « branche », on énumère tous les « sous-cas » possibles. Chaque « chemin » de la racine à la feuille, correspond à une issue possible. On énumère ainsi tous les cas, donc toutes les issues possibles.
1. Étude d’un exemple
Exercice résolu n°1
Une famille a deux enfants. On suppose qu’il y a autant de chances d’obtenir un garçon qu’une fille. (On suppose qu’il n’y a pas de jumeaux).
1°) Calculer la probabilité que « Obtenir deux filles ».
2°) Calculer la probabilité que « Obtenir deux enfants de sexes différents ».
3°) Calculer la probabilité que « Obtenir au moins un garçon ».
On appelle $F$ l’événement « obtenir une fille » et G l’événement « obtenir un garçon » à chaque naissance.
Chaque naissance correspond à un nœud, d’où partent des flèches indiquant tous les cas possibles, F ou G.
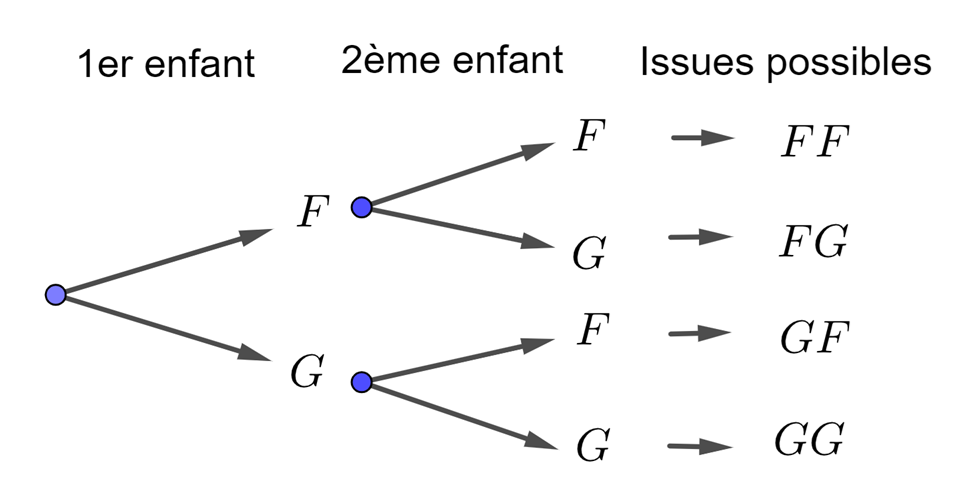
1er enfant 2ème enfant issues possibles
2. Nombre d’issues possibles
Étude d’un exemple pour illustrer
Prenons un exemple où l’on doit choisir entre plusieurs options à chaque étape. On considère une boîte de jeux en bois d’un enfant. On peut les ranger par couleur, par forme ou par taille.
Par exemple, si vous devez choisir une couleur parmi 3 options : rouge, vert, bleu ; puis une forme parmi 4 options : rond, carré, triangle, rectangle ; et enfin une taille parmi 2 options : petite, grande.
Chaque couleur contient 4 formes possibles et chaque forme contient 2 tailles possibles. Donc, dans ce cas, on applique le principe multiplicatif, l’arbre aurait $3\times 4 \times 2= 24$ issues possibles.
3. Exercices résolus
Exercice 2. A terminer
Une famille a trois enfants. On suppose qu’il y a autant de chances d’obtenir un garçon qu’une fille. (On suppose qu’il n’y a pas de jumeaux).
1°) Calculer la probabilité que « La famille obtient trois filles ».
2°) Calculer la probabilité que « La famille obtient deux enfants de sexes différents ».
3°) Calculer la probabilité que « La famille obtient au moins un garçon ».
Exercice 3. A terminer
On dispose de deux porte-monnaie identiques. Le premier contient 3 billet de 10€ et 5 billets de 20€. Le deuxième contient 2 billet de 10€ et 4 billets de 20€. On choisit au hasard un porte-monnaie, puis on tire à l’aveugle un billet de ce porte-monnaie.
1°) Dénombrer tous les cas possibles.
2°) Calculer la probabilité de tirer un billet de 10€.
3°) En déduire la probabilité de tirer un billet de 20€.

