Très souvent, on donne les mesures des trois côtés d’un triangle et on se demande si ce triangle est rectangle ou non. La réciproque du théorème de Pythagore donne une réponse positive à cette question.

Mais attention, on ne doit pas parler de « l’hypoténuse » tant qu’on ne sait pas s’il est rectangle ou non. On utilise le terme « plus grand côté ».

1. Réciproque du théorème de Pythagore

Réciproque du théorème de Pythagore.
Dans un triangle quelconque, Si le carré de la longueur du plus grand côté est égal à la somme des carrés des des longueurs des deux autres côtés, Alors ce triangle est rectangle et son plus grand côté est l’hypoténuse.

En général, on dit « dans un triangle, Si l’égalité du Pythagore est vraie, Alors ce triangle est rectangle et son plus grand côté est l’hypoténuse.
Que se passe-t-il sinon ? Voir plus bas.

Exercice résolu n°1.
Soit $IJK$ un triangle tel que $AB=4,5~$cm, $AC=6~$cm et $BC=7,5~$cm.
Le triangle $ABC$ est-il rectangle ? Si oui, préciser le sommet de son angle droit.

$ABC$ est un triangle tel que $AB=4,5~$cm, $AC=6~$cm et $BC=7,5~$cm.
Le plus grand côté est $[BC]$. On calcule séparément : $$\left\{\begin{array}{rl} &BC^2=7,5^2=\boxed{~56,25~}\\ \text{et} & AB^2+AC^2=4,5^2+6^2=20,25+36=\boxed{~56,25~}\\ \end{array}\right.$$
On constate que : $$BC^2=AB^2+AC^2$$ Donc, d’après la réciproque du théorème de Pythagore, le triangle $ABC$ est rectangle en $A$. CQFD.$\blacktriangle$

Haut de page

2. Contraposée du théorème de Pythagore

Contraposée du théorème de Pythagore.
Dans un triangle quelconque, Si le carré de la longueur du plus grand côté n’est pas égal à la somme des carrés des longueurs des deux autres côtés, Alors ce triangle n’est pas rectangle.

En général, on dit « dans un triangle, Si l’égalité du Pythagore est fausse, Alors ce triangle n’est pas rectangle. On ne peut plus parler d’hypoténuse.

3. Exercices résolus

Exercice résolu n°2.
Soit $IJK$ un triangle tel que $IJ=12~$cm, $IK=13~$cm et $JK=5~$cm.
Le triangle $IJK$ est-il rectangle ? Si oui, préciser le sommet de son angle droit.

$IJK$ est un triangle tel que $IJ=12~$cm, $IK=13~$cm et $JK=5~$cm.
Le plus grand côté est $[IK]$. On calcule séparément : $$\left\{\begin{array}{rl} &IK^2=13^2=\boxed{~169~}\\ \text{et} & IJ^2+JK^2=12^2+5^2=144+25=\boxed{~169~}\\ \end{array}\right.$$
On constate que : $$IK^2=IJ^2+JK^2$$ Donc, d’après la réciproque du théorème de Pythagore, le triangle $IJK$ est rectangle en $J$. CQFD.$\blacktriangle$

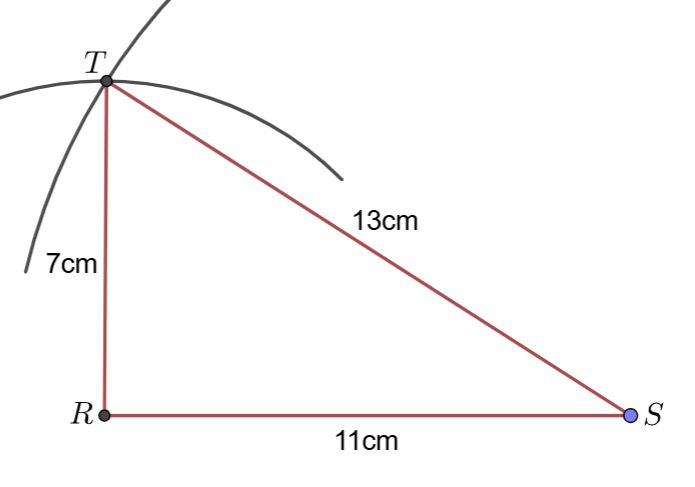
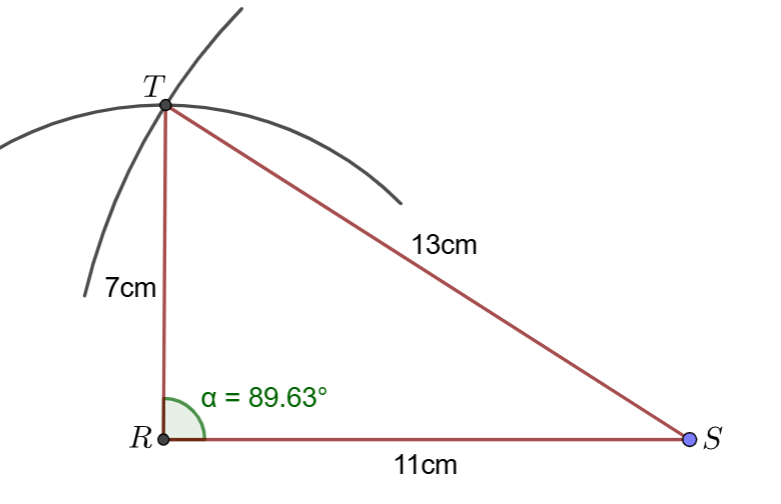
Exercice résolu n°3.
Soit $RST$ un triangle tel que $RS=11~$cm et $ST=13~$cm et $RT=7~$cm.
1°) Construire le triangle $RST$ à la règle et au compas.
2°) Que peut-on dire du triangle $RST$ ? Écrire une conjecture.
3°) Le triangle $IJK$ est-il rectangle ou non ? Si oui, préciser le sommet de son angle droit.

1°) On construit le triangle $RST$ à la règle et au compas.

Triangle non rectangle contraposée

2°) Conjecture,
« D’après la figure ci-dessus, à l’oeil nu et même avec un rapporteur, il semble que le triangle $RST$ soit rectangle en $R$ ».

3°) Vérifions si c’est le cas.
$RST$ est un triangle tel que $RS=11~$cm et $ST=13~$cm et $RT=7~$cm.
Le plus grand côté est bien $[ST]$. On calcule séparément : $$\left\{\begin{array}{rl} &ST^2=13^2=\boxed{~169~}\\ \text{et} & RS^2+RT^2=11^2+7^2=121+49=\boxed{~170~}\\ \end{array}\right.$$
On constate que : $$ST^2\not=RS^2+RT^2$$ Donc, d’après d’après la contraposée du théorème de Pythagore, le triangle $RST$ n’est pas rectangle. CQFD.$\blacktriangle$
———-
Remarques : On peut dire également :
On constate que : $$ST^2\not=RS^2+RT^2$$ Donc, l’égalité de Pythagore n’est pas vérifiée. Donc, d’après le théorème de Pythagore, le triangle $RST$ ne peut pas être rectangle. C’est absurde !
Avec Geogebra, j’ai mesuré l’angle $\hat R$ et j’obtiens : $$\widehat{SRT}=89,63^\circ$$ Donc le triangle $RST$ n’est pas rectangle.

Triangle non rectangle contraposée mesure d'angle
$\widehat{SRT}=89,63^\circ\not=90^\circ$

Haut de page