Théorème de Thalès dans le triangle. Agrandissement et Réduction

---

1. Triangles emboîtés

Définition 1.
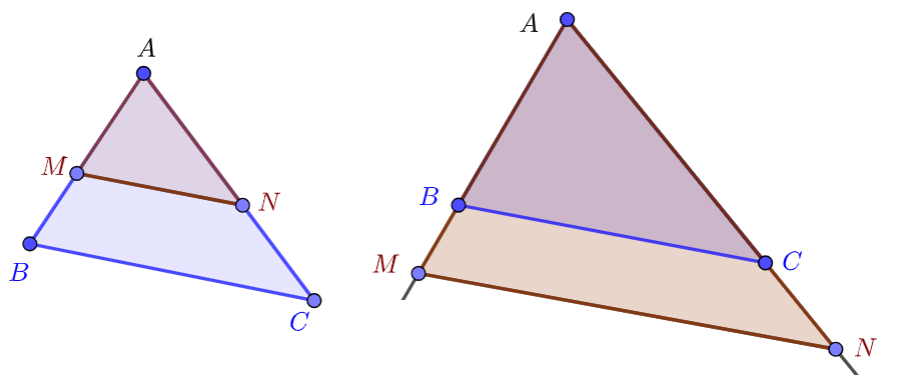
On dit que le triangle $AMN$ est emboîté dans le triangle $ABC$ de même sommet A, lorsque les deux autres sommets $M$ et $N$ appartiennent aux côtés $[AB]$ et $[AC]$ respectivement.
De même, le triangle $ABC$ est emboîté dans le triangle $AMN$ de même sommet A, lorsque les deux autres sommets $B$ et $C$ appartiennent aux côtés $[AM]$ et $[AN]$ respectivement. comme le montrent les figures ci-dessous.

Dans cette définition des triangles emboîtés, les droites $(MN)$ et $(BC)$ ne sont pas nécessairement parallèles.
Par contre, dans les configurations de Thalès de triangles emboîtés, les droites $(MN)$ et $(BC)$ sont parallèles.

1. Théorème de Thalès dans le triangle

Activité en classe

Tracer un triangle $ABC$, assez grand.
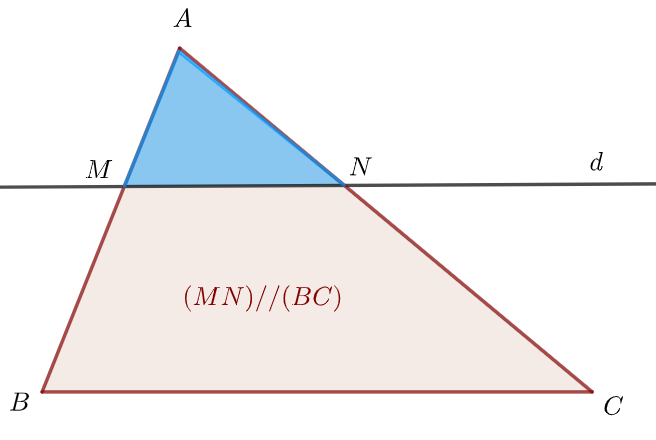
Puis tracer une droite $d$ parallèle au côté $[BC]$.
La droite $d$ coupe les côtés $[AB]$ et $[AC]$ en $M$ et $N$ respectivement. On obtient deux triangles. Un petit $AMN$ et un grand $ABC$. On cherche à déterminer si les longueurs des côtés correspondants des deux triangles $AMN$ et $ABC$ sont proportionnelles ?
Pour cela, mesurer puis faire un tableau des longueurs des six côtés.
$$\begin{array}{|r|c|c|c|}\hline
\text{petit triangle} & AM & AN & MN \\
& \cdots & \cdots & \cdots \\ \hline
& \cdots & \cdots & \cdots \\
\text{grand triangle} & AB & AC & BC \\ \hline
\end{array}$$
Puis calculer les rapports entre les longueurs des côtés correspondants. $\dfrac{\text{petit}}{\text{grand}}$. Que constatez-vous ? Énoncer une conjecture.

Les deux configurations de Thalès de triangles emboîtés se traitent de la même manière. Nous énonçons ici le théorème de Thalès dans la configuration où le triangle $AMN$ est emboîté dans le triangle $ABC$.

Théorème 1 de Thalès dans le triangle (version 1) :
Dans un triangle $ABC$ quelconque, Si $M$ est un point du côté $[AB]$, $N$ est un point du côté $[AC]$ et si les deux droites $(MN)$ et $(BC)$ sont parallèles, Alors les longueurs des côtés correspondants des deux triangles sont proportionnelles.

Pour vérifier si deux quantités sont proportionnelles, on vérifie s’il y a égalité des quotients des termes correspondants non nuls. Ce qui donne la deuxième version du Théorème de Thalès dans le triangle comme suit :

Théorème 1 de Thalès dans le triangle (version 2) :
Dans un triangle ABC quelconque, Si $M$ est un point du côté $[AB]$, $N$ est un point du côté $[AC]$ et si les deux droites $(MN)$ et $(BC)$ sont parallèles, Alors, il y a égalité des trois rapports : $$\boxed{~\dfrac{\text{petit}}{\text{grand}}\rightarrow \dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC} ~}$$

Avec des symboles :

Si $M\in[AB]$ , $N\in[AC]$ et si $(MN)//(BC)$,
Alors : $\dfrac{\text{petit}}{\text{grand}}\rightarrow$ $\boxed{~\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC} ~}$
On peut également écrire les rapports dans l’autre sens pour l’autre configuration : $\dfrac{\text{grand}}{\text{petit}}$.

Remarque

Nous remarquons ici que le théorème de la droite des milieux devient un cas particulier du théorème de Thalès avec $\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}=\dfrac{1}{2}$.

2. Agrandissement et Réduction

Théorème 2.
Dans un triangle $ABC$ quelconque, Si $M$ est un point du côté $[AB]$, $N$ est un point du côté $[AC]$ et si les deux droites $(MN)$ et $(BC)$ sont parallèles, Alors les longueurs des côtés correspondants des deux triangles sont proportionnelles. Par conséquent :

1°) Le triangle $AMN$ est une réduction du triangle $ABC$ et le coefficient de réduction est : $\boxed{~k=\dfrac{\text{petit}}{\text{grand}}~}$
2°) Et le triangle $ABC$ est un agrandissement du triangle $AMN$ et le coefficient d’agrandissement est : $\boxed{~k=\dfrac{\text{grand}}{\text{petit}}~}$.

---

4. Exercices résolus

Exercice résolu 1.
$LMN$ est un triangle tel que $LM=10~$cm, $LN=8~$cm et $MN=12~$cm.
On place le point $S$ sur le côté $[LN]$ tel que $LS=3~$cm, puis le point $R$ sur le côté $[LM]$ tel que les droites $(RS)$ et $(MN)$ soient parallèles.
1°) Calculer $LR$ puis $RS$. Justifier votre réponse.
2°) En déduire que le triangle $LRS$ est une réduction du triangle $LMN$ et déterminer le coefficient de réduction.

---

Exercice résolu 2.
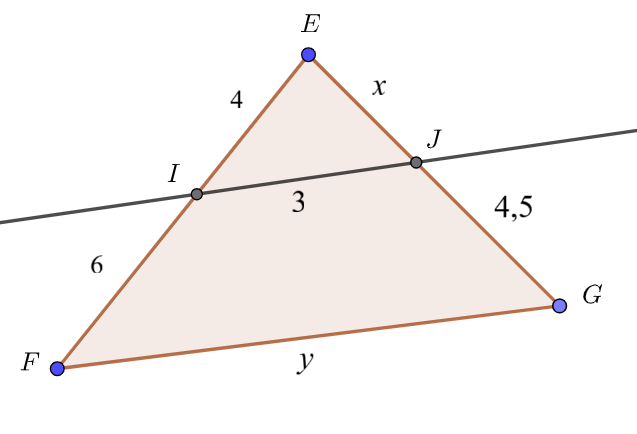
$EFG$ est un triangle coupé par une droite parallèle à (FG) et qui coupe $[EF]$ en $H$ et $[EG]$ en $K$.
On suppose que $EH=4~$cm, $HF=6~$cm, $KG=4,5~$cm et $HK=3~$cm. On pose $EK=x$ et $FG=y$.
1°) Faire une figure en reportant les mesures sur les côtés.
2°) Calculer $x=EK$
3°) Calcyuler $y=FG$.