1. Diagonale d’un polygone convexe
On se propose de définir des suites de nombres générées par des constructions géométriques utilisant ou non $n$-objets
Définition 1.
On appelle polygone convexe un polygone non croisé dans lequel on peut joindre deux points quelconques de ses ôtés sans sortir du polygone.
On appelle diagonale d’un polygone convexe un segment joignant deux sommets non consécutifs du polygone.
Par exemple, tous les polygones réguliers sont convexes.
2. Exemple
Suites de nombres générées par des constructions géométriques de diagonales dans un polygone régulier.
Exemple 1.
Soit $n$ un nombre entier supérieur ou égal à 2. On considère un polygone régulier $P_n$ (donc convexe) ayant $n$ côtés.
1°) Déterminer le nombre de diagonales dans un triangle équilatéral, un carré, un pentagone régulier et un hexagone.
2°) Soit $n$ un nombre entier supérieur ou égal à 2.
Déterminer une formule explicite ou récurrente donnant le nombre de diagonales dans un polygone régulier $P_n$ ayant $n$ côtés.
3°) Démontrer votre résultat en justifiant soigneusement.
3. Nombres triangulaires, nombres polygonaux
Suites de nombres générées par des constructions géométriques de triangles équilatéraux avec $n$ points dans chaque côté.
Définition 2.
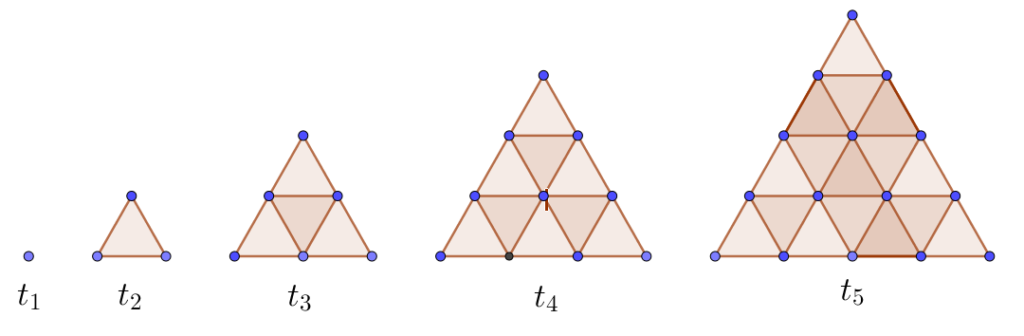
On appelle nombre triangulaire un nombre qui peut être représenté par un triangle équilatéral en disposant d’une certaine manière des cailloux ou des pois.
Un nombre triangulaire représenté par un triangle équilatéral de côté $n$ (caillous ou pois) se note $T_n$.
Suites de nombres générées par des constructions géométriques de de polygones réguliers à $p$ côtés avec $n$ points dans chaque côté.
Définition 3.
On appelle nombre carré un nombre qui peut être représenté par un carré.
Un nombre carré représenté par un carré de côté $n$ (caillous ou pois) se note $C_n$.
D’une manière analogue, on appelle nombre pentagonal (ou plus généralement un nombre polygonal) un nombre qui peut être représenté par un pentagone régulier (ou un polygone régulier à $p$ côtés).
Un nombre pentagonal (resp. polygonal) représenté par un pentagone (resp. polygone) régulier de côté $n$ (caillous ou pois) se note $P_n$.
4. Exemples
Exemple 2.
Soit $n$ un nombre entier non nul.
1°) Calculer $T_1$, $T_2$, $T_3$ et $T_4$.
2°) Déterminer une formule explicite ou récurrente donnant les nombres triangulaires $T_n$.
3°) Démontrer votre résultat en justifiant soigneusement.
Exemple 3.
Même exercice que l’exercice 2 avec
1°) Les nombres carrés (trop facile)
2°) Les nombres pentagonaux.
3°) Les nombres hexagonaux.