Suite numérique définie par un algorithme en fonction de $n$

1. Suite numérique définie par un algorithme en fonction de $n$

Donner une suite numérique $(u_n)$ définie par un algorithme en fonction de $n$, revient à définir une fonction dans Python. Nous distinguons deux cas suivant que la suite est explicite ou récurrente.

1.1. Calcul de valeurs d’une suite explicite par un algorithme en fonction de $n$

Pour définir une fonction dans Python, on a besoin d’abord d’importer la ou les bibliothèque(s) nécessaire(s) pour le traitement du programme.

Par exemple. On utilise l’instruction « from math import sqrt » pour utiliser la fonction racine carrée, ou « from math import * » si on doit utiliser plusieurs fonctions ou constantes (comme $\pi$) dans cette bibliothèque.
De même, on utilise l’instruction « from randon import random» pour utiliser la fonction nombre aléatoire, ou « from random import * ».

Définition 1.
Soit $(u_n)$ la suite numérique explicite définie pour tout entier $n$ par : $u_n=3n-4$.
On se propose de définir une fonction qui affiche le 10ème terme de la suite $(u_n)$.
La syntaxe d’une fonction qui donne le $n$-ème terme de la suite $(u_n)$ est la suivante :

def u(n) :
_ _ _ _ y=expression de $u(n)$ en fonction de $n$
_ _ _ _return y
print(u(10))

Les 4 tirets _ _ _ _ correspondent à un alinéa ou une tabulation de 4 espaces.
Dans une ligne, un hachtag # précède un commentaire d’explication.

1.2. Exemples

Exemple 1.
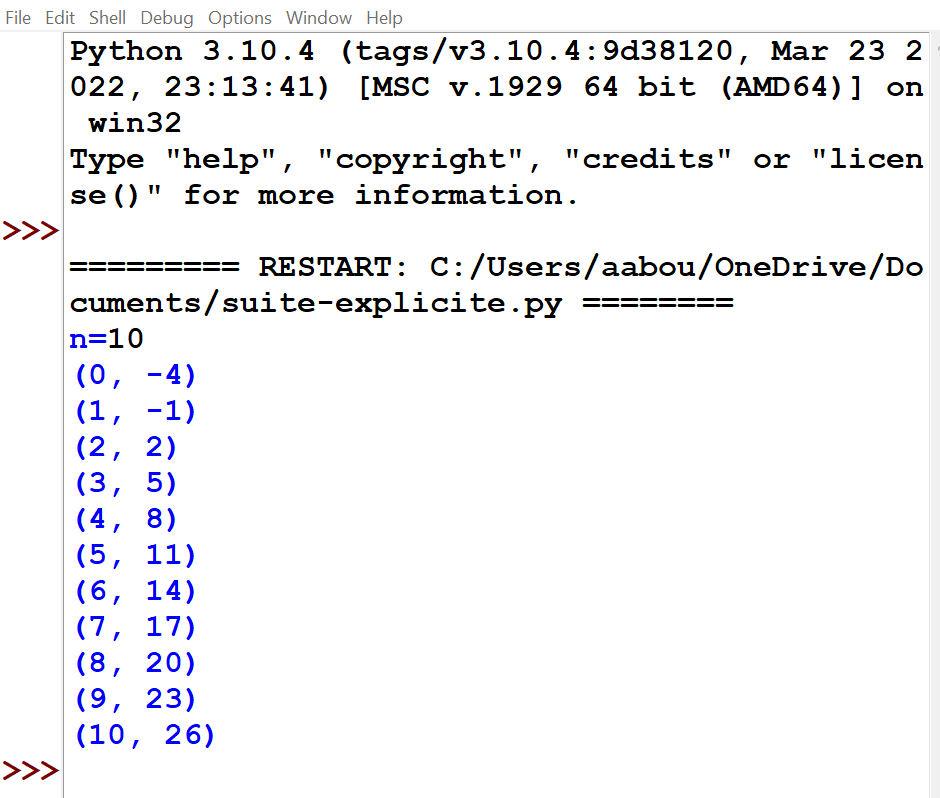
Soit $(u_n)$ la suite numérique (explicite) définie pour tout entier $n$ par : $u_n=3n-4$.
1°) Construire un algorithme qui permet d’afficher la valeur $u_{20}$.
2°) Modifier cet algorithme pour qu’il affiche toutes les valeurs de $u_n$, pour $n$ allant de $0$ à $10$.

---

Exemple 2.
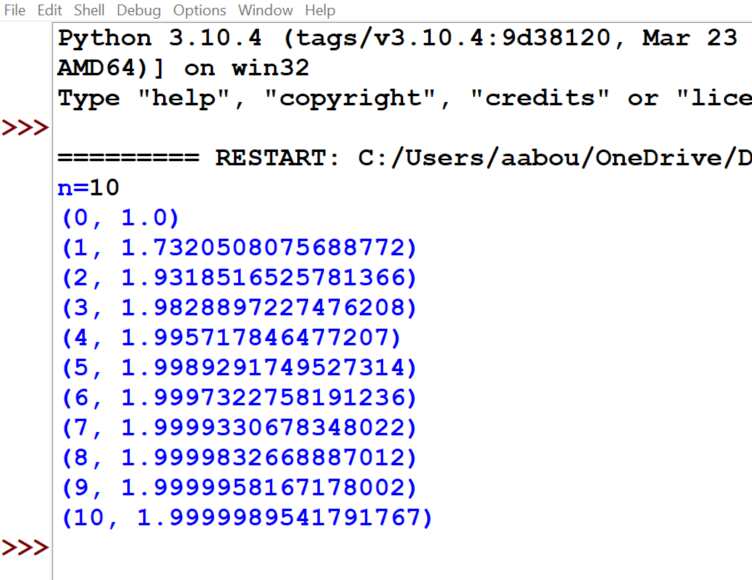
On considère la suite définie par récurrente par : $$\left\{ \begin{array}{l}u_0=-1, \text{ et pour tout entier }n\geq1 :\\ u_n=\sqrt{u_{n-1}+2}\\ \end{array}\right.$$
1°) Construire un algorithme qui permet d’afficher la valeur $u_{20}$.
2°) Modifier cet algorithme pour qu’il affiche toutes les valeurs de $u_n$, pour $n$ allant de $0$ à $10$.