La plupart des exercices ou de problèmes sur les probabilités au Brevet des collèges, sont situés dans l’exercice n°1 sous la forme de questions courtes ou d’affirmation qu’il faut confirmer ou réfuter avec ou sans justification. Également, on trouve dans l’exercice 5 de petits problèmes de la vie courante, où la rédaction tient une place importante.
A titre d’illustration, nous avons extrait ces exercices des annales de 2024 et 2025 du site de l’APMEP, Annales du Brevet des Collèges.

1. Affirmations ou questions courtes

DNB — Amérique du Nord — 4 juin 2025

Exercice résolu 1.
Dans une urne de 40 boules indiscernables au toucher, 5 sont rouges, 20 sont vertes et 15 sont blanches. On considère l’expérience qui consiste à tirer au hasard une boule de l’urne et à noter sa couleur.
Question : Calculer la probabilité d’obtenir une boule verte.

La probabilité est égale à $\dfrac{20}{40}=\dfrac{1}{2}=0,5$.

Haut de page

DNB — Amérique du Nord. Ex1. — 29 mai 2024.

Exercice résolu 2.
Une urne contient 15 boules indiscernables numérotées de 1 à 15.
On vous demande de dire si l’affirmation suivante est vraie ou fausse. Et on rappelle que chaque réponse doit être justifiée.
Affirmation. La probabilité de tirer au hasard une boule sur laquelle apparaît un nombre premier est $\dfrac{7}{15}$.

Une urne contient 15 boules indiscernables numérotées de 1 à 15.

Les nombres premiers inférieurs à 15 sont : 2 ; 3 ; 5 ; 7 ; 11 ; 13 : il y en a donc 6 parmi les 15, soit une probabilité de $\dfrac{6}{15}=\dfrac{2}{5}\not=\dfrac{7}{15}$.
L’affirmation est Fausse.

Haut de page

DNB — Centres étrangers. Ex1. — 10 juin 2024.

Exercice résolu 3.
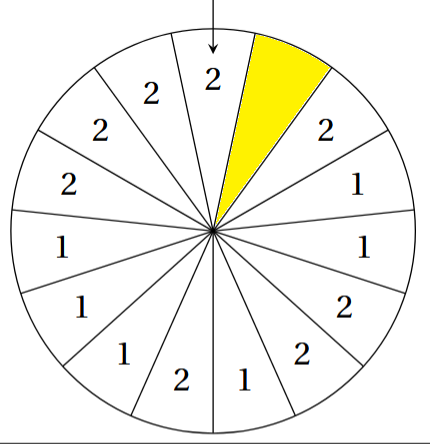
Sam fait tourner la roue ci-contre et regarde le nombre désigné par la flèche, qui peut être 1 ou 2.
On admet que chaque secteur a autant de chance d’être désigné.
Le nombre écrit dans le secteur jaune a été effacé. Est-il possible d’écrire un nombre dans ce secteur de sorte que la probabilité que la flèche désigne le nombre 2 soit égale à $\dfrac{3}{5}$ ?
Justifiez votre réponse.

La roue à secteurs tourne
La roue tourne

Réponse : Oui, en écrivant le nombre 2.
En effet, on suppose que chaque secteur a autant de chance d’être désigné, nous sommes en situation d’équiprobabilité. Avec 15 secteurs, la probabilité de désigner un secteur est de $\dfrac{1}{15}$. D’autre part : $\dfrac{3}{5}=\dfrac{9}{15}$.
Comme 8 des secteurs portent le numéro 2, en inscrivant 2 dans le secteur jaune où le nombre a été effacé, on aura 9 secteurs favorables à l’évènement sur 15, donc une probabilité de $\dfrac{9}{15}$, soit en simplifiant par 3 : $\dfrac{3}{5}$.

Haut de page

2. Petits problèmes de probabilités

DNB — Métropole Antilles Guyane. Ex1. — 26 juin 2025

Exercice résolu 4.
On dispose d’une urne A contenant 6 boules numérotées : 7 ; 10 ; 12 ; 15 ; 24 ; 30 ; et d’une urne B contenant 9 boules numérotées : 2 ; 5 ; 6 ; 8 ; 17 ; 18 ; 21 ; 22 ; 25.
Les boules sont indiscernables au toucher.

1. On tire une boule dans l’urne A, quelle est la probabilité d’obtenir un nombre pair ?
2. On tire une boule dans l’urne B, justifier que la probabilité d’obtenir un nombre premier est de $\dfrac{1}{3}$.
3. Quelle urne contient le plus grand nombre de boules dont le numéro est un multiple de 6 ?
4. On tire une boule au hasard dans l’une des urnes. Démontrer que la probabilité d’obtenir un nombre supérieur ou égal à 20 est la même quelle que soit l’urne choisie.
5. En repartant avec la composition initiale des urnes A et B on décide d’ajouter une boule numérotée 50 dans chacune d’entre elles. Dans ces conditions, la probabilité d’obtenir un résultat supérieur ou égal à 20 est-t-elle toujours égale quelle que soit l’urne choisie ?

1. Il y a 4 nombres pairs sur 6 nombres : la probabilité est donc égale à $\dfrac{4}{6}=\dfrac{2}{3}$.
2. Les nombres premiers sont : 2 ; 5 ; 17 : la probabilité est donc égale à $\dfrac{3}{9}=\dfrac{1}{3}$.
3. Dans l’urne A, $12=6\times2$ ; $24=6\times4$ et $30=6\times5$ sont des multiples de $6$.
Dans l’urne B, $6=6\times1$ ; $18=6\times3$ sont des multiples de $6$.
C’est donc l’urne A qui contient le plus grand nombre de multiples de $6$.
4. Dans l’urne A il y a 2 nombres supérieurs ou égaux à 20 : la probabilité est égale à $\dfrac{2}{6}=\dfrac{1}{3}$.
Dans l’urne B, il y a 3 nombres supérieurs ou égaux à 20 : la probabilité est égale à $\dfrac{3}{9}=\dfrac{1}{3}$. Les deux probabilités sont égales.
5. Le tirage dans l’urne A a une probabilité de celui dans l’urne B aura une probabilité
de $\dfrac{4}{10}=0,4$.
Or $\dfrac{3}{7}=0, 428, les probabilités ne sont plus égales.

Haut de page

DNB — Centres étrangers Groupe I — 16 juin 2025.

Exercice résolu 5.
Un digicode commande l’ouverture de la porte d’entrée de la maison de la grand-mère de
Léna. Léna a oublié le code. Elle sait qu’il est composé d’une lettre A, B, ou C, suivie d’un chiffre
compris entre 0 et 9.

1°) Proposer deux codes différents que Léna peut tester.
2°) Quelle est la probabilité que la grand-mère de Léna ait choisi la lettre C dans son code ?
3°) Montrer que la probabilité que la grand-mère de Léna ait choisi le chiffre 7 dans son code est $\dfrac{1}{10}$.
4°) Léna se souvient que sa grand-mère, enseignante de mathématiques à la retraite, aime bien les nombres premiers. Quelle est la probabilité que le code choisi par sa grand-mère comporte un nombre premier ?

5. a) Léna décide de tester tous les codes possibles. Elle estime qu’il lui faut 5 secondes pour essayer un code. Réussira-t-elle à ouvrir la porte de la maison en moins de 3 minutes ?
b) Le format de ce code garantit-il la sécurité de la maison ? Comment pourrait-on améliorer ce système de code ?

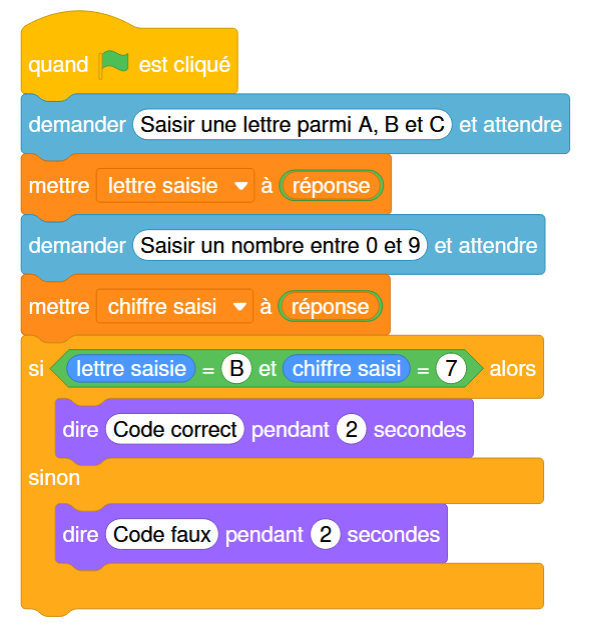
6. Chaque fois qu’un utilisateur saisit un code, un programme lui annonce si le code est correct ou faux. Le programme utilisé est noté ci-dessous.
a) Léna saisit le code B5. Qu’affiche le programme ?
b) D’après ce programme, quel est le code qui permet d’entrer dans l’immeuble de la grand-mère de Léna ?

DNB-Centres étrangers Groupe I-Ex5-16 juin 2025
image APMEP

1. B3 ou C9 sont des codes possibles
2. On peut choisir entre 3 lettres puis entre 10 chiffres : il y a donc $3\times10=30$ codes
possibles différents.
Il y a $10$ codes commençant par C : la probabilité que le code commence par la lettre
C est donc : $\dfrac{10}{30}=\dfrac{1}{3}$.
3. Il y a trois codes se finissant par 7 : A7, B7 et C7.
La probabilité que le code se finisse par 7 est égale à $\dfrac{3}{30}=\dfrac{1}{10}=0,1$.
4. Les nombres 2, 3, 5 et 7 sont premiers : il y a 3 codes finissant par l’un de ces 4 nombres, soit $3\times4 = 12$ codes contenant un nombre premier.
La probabilité que le code contienne un nombre premier est donc égale à $\dfrac{12}{30}=\dfrac{\not6\times2}{\not6\times5}=\dfrac{2}{5}=0,4$.
5. a) Avec 30 codes différents il lui faudra au maximum : $30\times5=150~$s, soit $120+30~$s ou $2~$min $30~$s, donc en moins de $3~$min.
b) N’importe qui peut trouver le code en $2~$min $30~$s maximum : c’est insuffisant.
En prenant l’une des $26$ lettres de l’alphabet, il faudra $26\times5\times3=390~$s, soit $6~$min $30~$s, soit en plus de deux fois plus de temps.
6. a) B5 n’est pas le code attendu ; le programme affiche Code faux.
b) Le code attendu est B7.

Haut de page