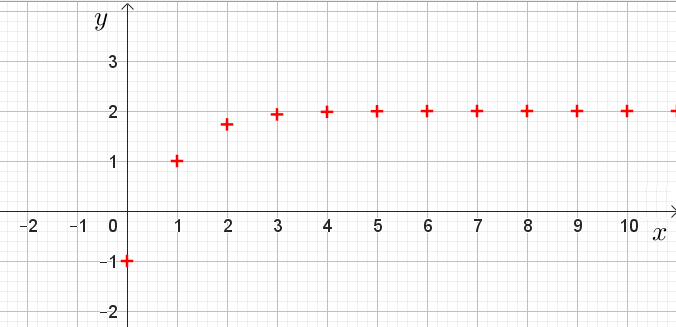
La représentation graphique d’une suite numérique permet de donner le sens de variation et de donner la tendance des valeurs de la suite lorsque $n$ tend vers l’infini.
1. Représentation graphique d’une suite numérique
On veut construire la représentation graphique d’une suite numérique. Alors on se se donne un repère $(O,\vec{\imath}, \vec{\jmath})$ orthonormé ou non.
Définition 1.
Soit $(u_n)$ une suite numérique. Alors la représentation graphique d’une suite numérique dans le repère $(O,\vec{\imath}, \vec{\jmath})$, est l’ensemble des points $A(n;u_n)$ du plan dont les abscisses sont les nombres entiers naturels $n$ (ou à partir d’un certain rang) et d’ordonnées $u_n$.
Remarque
Contrairement à une fonction de la variable réelle, la représentation graphique d’une suite numérique n’est pas une ligne courbe, mais un ensemble de points. Par conséquent, une représentation graphique d’une suite numérique sera matérialisée par une suite de croix « $\times$ » ou de signes plus « $+$ » ou de puces « $\bullet$ ».
2. représentation graphique d’une suite explicite
Définition 2. (suite explicite)
Soit $(u_n)$ une suite explicite définie pour tout entier $n$ par : $$u_n=f(n)$$ Alors, la représentation graphique de la suite explicite $(u_n)$ est l’ensemble des points $A(n;u_n)\in{\mathcal C}_f$ dont les abscisses sont des nombres entiers. Donc, on construit un tableau de valeurs avec un tableur ou une calculatrice, puis on construit la courbe à la main ou à l’aide d’un logiciel tel que Geogebra.
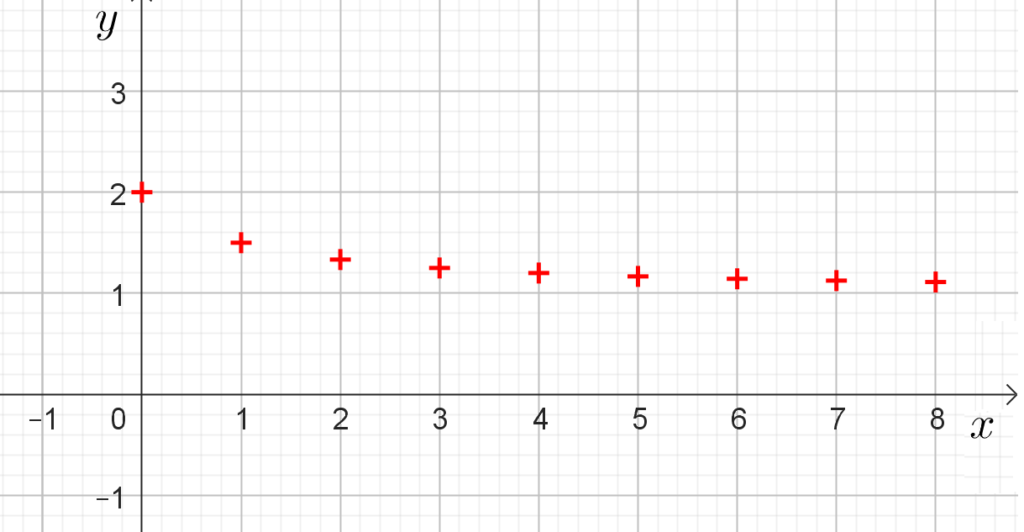
Représentation graphique de la suite explicite : $u_n=\dfrac{1}{n+1}+1$.
2. représentation graphique d’une suite récurrente
Définition 3. (suite récurrente)
Soit $(u_n)$ une suite explicite définie pour tout entier $n$ par : $$u_n=f(n)$$ Alors, la représentation graphique de suite explicite $(u_n)$ est l’ensemble des points $A(n;u_n)$. On a donc :
$\bullet$ La construction avec un tableur ou Géogebra, voir procédure ci-dessous.
$\bullet$ La construction à la main exige une manipulation géométrique :
- On place $u_0$ sur l’axe des abscisses puis on calcule $u_1=f(u_0)$ qui est sur l’axe des ordonnées.
- Avec un compas ou par symétrie par rapport à la première bissectrice (droite d’équation $y=x$ dans un repère $(O,\vec{\imath}, \vec{\jmath})$), on reporte la valeur $u_1=f(u_0)$ sur l’axe des abscisses.
- Puis on recommence le procédé.
- On peut aussi utiliser la droite $y=x$ comme miroir de réflexion de la lumière entre la courbe et la droite. Ce qui permet de placer les valeurs $u_0$, $u_1$, $u_2$, $u_3$, etc. sur l’axe des abscisses. [Question souvent posée au Bac.]
Voir exercice 2.
2. Méthode avec un tableur ou sur Géogebra
- Ouvrir un Tableur
- ou Ouvrir Geogebra puis dans « Affichage », cliquer sur « Tableur »
- Dans la cellule A1, taper « n » puis 0 dans A2 et 1 dans A3
- Sélectionner les deux cellules A1 et A3, puis tirer sur la poignée en bas à droite de la sélection jusqu’à « $n=17$ » par exemple. Vous obtenez la liste des nombres entiers de 0 à 15.
- Dans la cellule B1, taper « u_n »
- Pour une suite explicite :
Dans la cellule B2, taper la formule de « u_n » en remplaçant « $n$ » par « A2 »
Pour une suite récurrente :
Taper la valeur de $u_0$ dans la cellule B2
Dans la cellule B3, taper la formule de « u_n » en remplaçant « $n$ » par « B1 » - Puis Sélectionner « B2 » (explicite) ou « B3 » (récurrente), puis tirer sur la poignée jusqu’à « $n=17$ » par exemple. Vous obtenez la liste des nombres valeurs $u_n$ pour $n$ variant de 0 à 15.
- Sélectionner maintenant le tableau de valeurs de la cellule A2 à B17.
- Faites un « Clic droit » puis sélectionner « Créer » puis à gauche cliquez sur « Liste de points ».
- Supprimes l’affichage des étiquettes des points (sauf si c’est déjà fait par défaut.
- Vous réajustez les unités pour obtenir un affichage avec le nombre de points qui vous convient.
- Enfin, Exportez votre fichier en .png ou en LaTeX pour l’insérer dans votre document.
3. Exercices
Exemple 1.
Dans un repère orthonormé $(O,\vec{\imath}, \vec{\jmath})$, on considère la suite récurrente définie par : $$\left\{ \begin{array}{l}u_0=-1, \text{ et pour tout entier }n\geq1 :\\ u_n=\sqrt{u_{n-1}+2}\\ \end{array}\right.$$
1°) Construire la courbe représentative de la suite $(u_n)$ avec un tableur ou Geogebra.
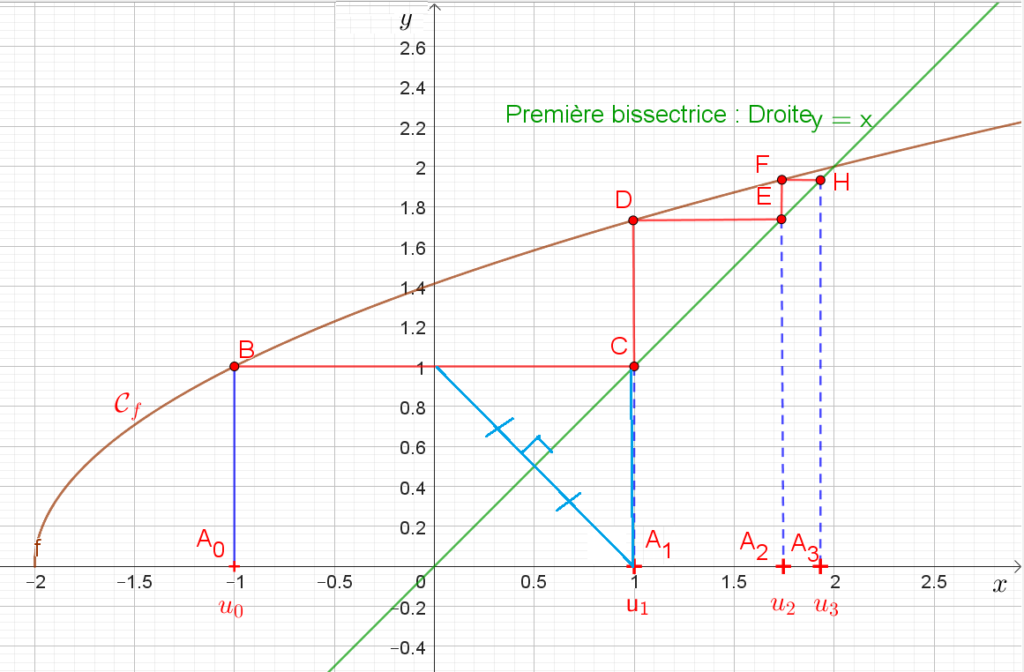
2°) Construire la courbe représentative de la fonction associée $f$ définie sur $[-2;+\infty[$ par : $$f(x)=\sqrt{x+2}$$ $\quad$Puis en déduire une construction géométriques pour placer les valeurs $u_0$, $u_1$, $u_2$ et $u_3$ sur l’axe des abscisses.
1°) Avec un tableur ou Geogebra
Utiliser la procédure précédente avec un tableur ou Geogebra pour construire la courbe représentative de la suite récurrente définie par : $(u_n)$
2°) Recherche des valeurs des termes de la suite sur le graphique de la courbe de la fonction associée $f$ définie sur $[-2;+\infty[$ par : $$f(x)=\sqrt{x+2}$$
$\bullet$ On place le terme $u_0=-1$ sur l’axe des abscisses ;
$–$ On calcule $u_1=f(u_0)=1$ qui est sur l’axe des ordonnées.
$–$ En utilisant la symétrie par rapport à la première bissectrice (droite d’équation $y=x$ dans le repère orthonormé $(O,\vec{\imath}, \vec{\jmath})$), on reporte la valeur $u_1=f(u_0)=1$ sur l’axe des abscisses, puis on calcule son image.
Et ainsi de suite.
On peut aussi suivre les segments rouges joignant les points $A$, $B$, $C$, etc.
Ce qui revient à utiliser la droite $y=x$ comme miroir de réflexion de la lumière entre la courbe et la droite. Ce qui permet de placer les valeurs $u_0$, $u_1$, $u_2$, $u_3$, etc. sur l’axe des abscisses. [Question souvent posée au Bac.]