On veut construire la représentation graphique d’une suite numérique. Alors on se donne un repère $(O,\vec{\imath}, \vec{\jmath})$ orthonormé ou non. On construit d’abord un tableau de valeurs $(n, u_n)$ à la main, à la calculatrice, avec un tableur ou à l’aide de Geogebra.

Sommaire

  1. Représentation graphique d’une suite arithmétique
  2. Représentation graphique d’une suite arithmétique et fonction affine associée

1. Représentation graphique d’une suite arithmétique

Définition 1.
Soit $(u_n)$ une suite arithmétique. Alors sa représentation graphique dans le repère $(O,\vec{\imath}, \vec{\jmath})$, est l’ensemble des points $A(n;u_n)$ du plan.

Propriété 1.
L’ensemble des points représentatifs des termes d’une suite arithmétique $(u_n)$, sont tous alignés, donc situés sur une même droite $D$.

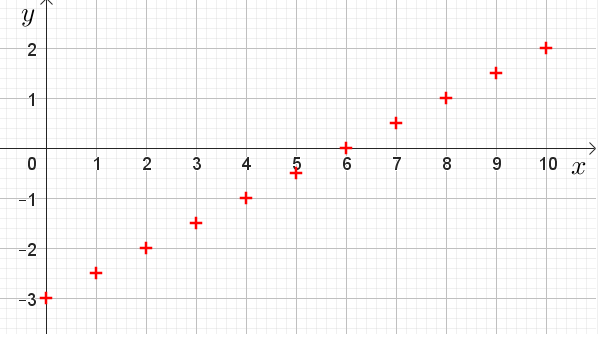
Exemple 1.
Soit $(u_n)$ la suite arithmétique de raison $r=\dfrac{1}{2}$ et de premier terme $u_0=-3$.
Construire la représentation graphique de la la suite $(u_n)$ dans le repère orthonormé $(O,\vec{\imath}, \vec{\jmath})$.

1°) Avec un tableur ou Geogebra
Utiliser la procédure précédente avec un tableur ou Geogebra pour construire la courbe représentative de la suite $(u_n)$. L’expression explicite de la suite $(u_n)$ est donnée par : $$u_n=-3+\dfrac{1}{2}n$$
On construit d’abord un tableau de valeurs $(n, u_n)$ à la calculatrice, avec un tableur ou à l’aide de Geogebra : $$\begin{array}{|c|c|}\hline n & u_n\\ \hline
0& -3\\ \hline 1& -2.5\\ \hline 2& -2\\ \hline 3& -1,5\\ \hline 4& -1\\ \hline 5& -0.5\\ \hline 6& 0\\ \hline 7& 0.5\\ \hline 8& 1\\ \hline 9& 1,5\\ \hline 10&2 \\ \hline \end{array}$$

2. Représentation graphique d’une suite arithmétique et fonction affine associée

Propriété 2.
Soit $(u_n)$ une suite arithmétique et
Les points représentatifs des termes d’une suite arithmétique $(u_n)$, sont tous alignés, donc situés sur une même droite $D$.
La droite $D$ est la représentation graphique de la fonction affine associé à la suite arithmétique $(u_n)$.

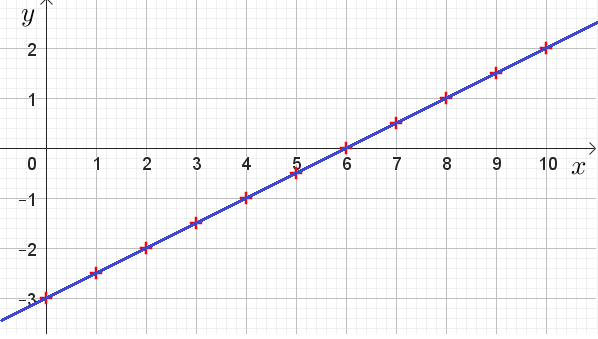
Exemple 2. Illustration.
Soit $(u_n)$ la suite arithmétique de raison $r=\dfrac{1}{2}$ et de premier terme $u_0=-3$.
1°) Déterminer l’expression de la fonction affine associé à la suite arithmétique $(u_n)$ dans le repère orthonormé $(O,\vec{\imath}, \vec{\jmath})$.
2°) Construire la représentation graphique de la fonction affine associé à la suite arithmétique $(u_n)$.
3°) Construire la représentation graphique de la la suite $(u_n)$ dans le même repère $(O,\vec{\imath}, \vec{\jmath})$.
4°) Que constatez-vous ?

1°) Expression de la fonction affine
L’expression explicite de la suite $(u_n)$ est donnée par : $$u_n=-3+\dfrac{1}{2}n$$ Donc, l’expression de la fonction affine $f$ associé est : $$f(x) = -3+\dfrac{1}{2}x$$ pour tout $x\in\R$.

2°) Construction de la droite représentative de $f$
Pour construire la droite représentative $D$ de $f$, il suffit de trouver deux points. (je prends des valeurs paires pour simplifier).
Pour $x=0$ : $f(0)=-3$. Donc le point $A(0;-3)\in D$.
Pour $x=4$ : $f(4)=-1$. Donc le point $A(4;-1)\in D$.

3°) Avec un tableur ou Geogebra, on construit la courbe représentative (suite des points en rouge) de la suite $(u_n)$.

4°) Que constatez-vous ?
Tous les points représentatifs de la suite $(u_n)$ sont situés sur la droite $D$, représentation graphique de la fonction affine associé $f$.