1. Repère orthogonal, repère orthonormé
Définitions 1.
Trois points distincts $O$, $I$ et $J$ non alignés forment un repère $(O\, ; I, J)$ du plan.
Tout point $M$ du plan est « repérés » par un couple de deux coordonnées $(x,y)$.
$x$ est l’abscisse du point $M$ et $y$ est l’ordonnée du point $M$.
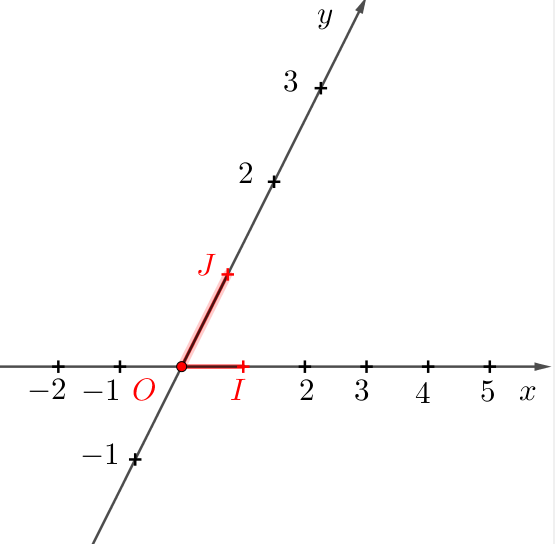
Si les points $O$, $I$ et $J$ sont alignés, ils appartiennent à une même droite du plan, donc ne définissent pas un repère du plan.
Si $O$, $I$ et $J$ sont non alignés, ils forment un triangle. Donc ils définissent un repère $(O\, ; I ; J)$ du plan.
$\quad\bullet$ Le point $O $ est l’origine du repère ;
$\quad\bullet$ $(OI)$ est l’axe des abscisses et $OI$ est l’unité de la graduation sur cet axe.
$\quad\bullet$ $(OJ)$ est l’axe des ordonnées et $OJ$ est l’unité de la graduation sur cet axe.
Définitions 2.
1°) On dit qu’un repère $(O\, ;I, J)$ est orthogonal (r.o.g) si et seulement si les deux axes $(OI)$ et $(OJ)$ sont perpendiculaires.
2°) On dit qu’un repère $(O, I, J)$ est orthonormé (r.o.n) ou orthonormal si et seulement si :
$\quad\bullet$ les deux axes $(OI)$ et $(OJ)$ sont perpendiculaires : $(OI) \bot (OJ)$
$\quad\bullet$ Et les unités sur les deux axes sont égales : $OI = OJ$.
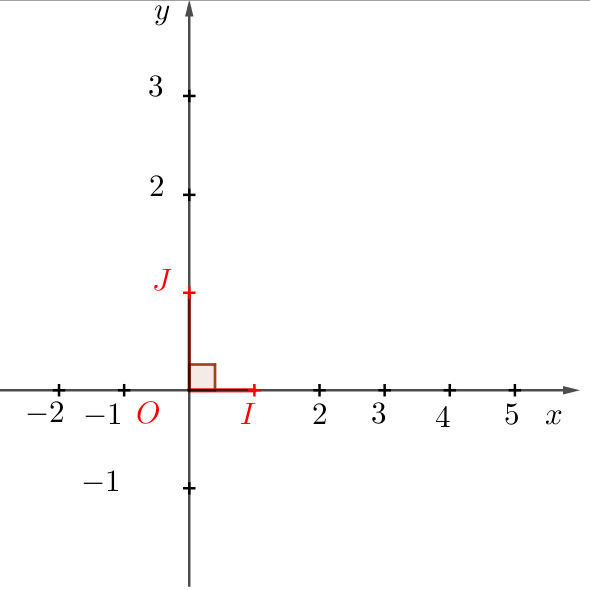
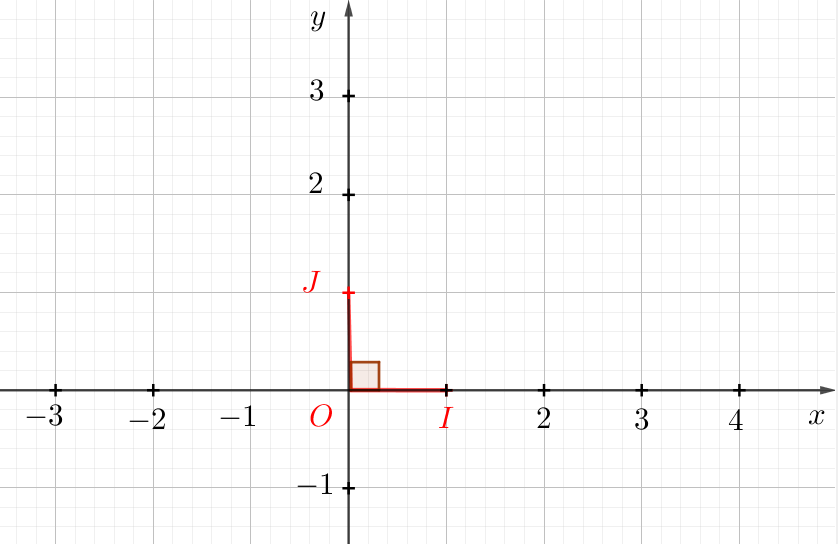
Remarque
Définir un repère orthonormé du plan revient à définir un triangle $OIJ$ rectangle isocèle en $O$. Ce qui équivaut à : $(OI) \bot (OJ)$ et $OI = OJ$.
2. Coordonnées d’un point dans le plan
Théorème 1.
Soit $(O\, ; I ; J)$ un repère quelconque du plan. Tout point $M$ du plan est repéré par un couple $(x_M;y_M)$ de nombres réels appelés les coordonnées du point $M$.
La première composante $x_M$ est l’abscisse de $M$ et se lit sur l’axe horizontal.
La deuxième composante $y_M$ est l’ordonnée de $M$ et se lit sur l’axe vertical.
Remarques
1°) Les mots abscisse, ordonnée et coordonnée sont des mots féminins.
2°) Dans le repérage des points du plan, les coordonnées et les axes sont rangés (naturellement) par ordre alphabétique :
| 1ère coordonnée | < | 2ème coordonnée |
| $x$ | $y$ | |
| axe horizontal | axe vertical | |
| abscisse | ordonnée | |
| antécédent | image | |
| cosinus | sinus |
3. Exercices
Exercice résolu n°1. Dans la figure suivante, le plan est muni d’un repère orthonormé.
Lire les coordonnées des points indiqués : $O$, $A$, $B$, $C$, $D$, $E$, $F$ et $G$.


