Les suites géométriques jouent un rôle important en mathématiques comme modèles discrets d’évolutions relatives constantes à croissance exponentielle. D’autres part, ce sont des suites qui s’expriment sous une forme récurrente et sous une forme explicite, mais aussi avec une fonction exponentielle associée.
Sommaire
1. Propriétés des suites géométriques
2. Sommes de termes consécutifs d’une suite géométrique
2.1. Nombre de termes consécutifs entre deux rangs d’une suite
2.2. Somme des termes consécutifs d’une suite géométrique
1. Propriétés des suites géométriques
Propriété 1.
Soit $(v_n)$ une suite géométrique de raison $q$ et de premier terme $v_0\not=0$. Alors la forme récurrente de la suite $(v_n)$ est donnée pour tout entier $n\geqslant0$ par : $$(P_1)\quad\boxed{~\left\{\begin{array}{l} v_0\in\R\text{ est donné}\\ v_{n+1}=v_n\times q\\ \end{array}\right.~}$$
Propriété 2.
Soit $(v_n)$ une suite géométrique de raison $q$ et de premier terme $v_0\not=0$. Alors la forme explicite de la suite $(v_n)$ est donnée pour tout entier $n\geqslant0$ par : $$(P_2)\quad\boxed{~v_{n}=v_0\times q^n~}$$
Définition 1.
Soit $(v_n)$ une suite géométrique. On appelle éléments caractéristiques de la suite $(v_n)$, sa raison $q$ et son premier terme $v_0$.
Propriété 3.
Soit $(v_n)$ une suite géométrique de raison $q$ et de premier terme $v_0\not=0$. Alors la connaissance de deux termes de la suite permet de connaitre les éléments caractéristiques de cette suite $(v_n)$.
Pour tout entier $n\geqslant0$ et tout $p\geqslant0$ on a : $$(P_3)\quad\boxed{~v_{n}=v_{p}\times q^{n-p}~}$$ qu’on pourrait également écrire (sachant que tous les $v_n\not=0$) : $$(P_{3\,\text{bis}})\quad\boxed{~\dfrac{v_{n}}{v_{p}}=q^{n-p}~}$$
En effet : $$\begin{array}{rcl}
v_n&=&v_0\times q^n\quad(1)\\
v_p&=&v_0\times q^p\quad(2)\\ \hline
\end{array}$$ Tous les $v_n\not=0$, donc en divisant membre à membre les 2 égalités $(1)$ par $(2)$, on obtient : $\dfrac{v_{n}}{v_{p}}=\dfrac{v_0\!\!\! /\times q^n}{v_0\!\!\! /\times q^p}=\dfrac{q^n}{q^p}=q^{n-p}$. D’où : $\boxed{~\dfrac{v_{n}}{v_{p}}=q^{n-p}~}$ ou encore : $\boxed{~v_{n}=v_{p}\times q^{n-p}~}$
Exemple 1.
Soit $(v_n)$ une suite géométrique. On connaît deux termes : $v_{3}=18$ et $v_{5}=40,25$.
Déterminer les éléments caractéristiques de la suite $(v_n)$. C’est-à-dire :
1°) Déterminer la raison de la suite géométrique $(v_n)$.
2°) En déduire le premier terme $v_0$ de la suite $(v_n)$.
2. Sommes de termes consécutifs d’une suite
2.1. Nombre de termes consécutifs entre deux rangs d’une suite
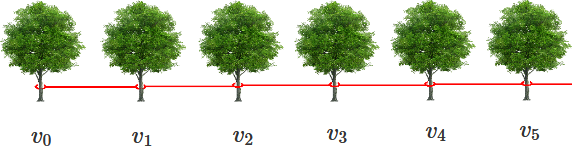
Commençons par dénombrer (compter le nombre) des termes :
$\rightarrow$ De 0 à 5 il y a 6 termes, alors que : $5 – 0 = 5$ = nombre de raisons, ou d’intervalles.
$\rightarrow$ Par contre, le nombre de termes = $6 = 5 – 0 +1$ = le nombre de « cordes ».
Finalement, le nombre de termes = différence des rangs$+1$.
Proposition 1.
Soit $(u_n)$ une suite numérique. Alors le nombre de raisons de $u_p$ à $u_n$ $(n>p)$ est égal à $n-p$ et le nombre de termes de $u_p$ à $u_n$ est égal à $n-p+1$.
Exemple 2.
Soit $(v_n)$ une suite numérique. Combien y a-t-il de termes entre $u_4$ et $u_{17}$ ?
2.2. Somme des termes consécutifs d’une suite géométrique
Très souvent, nous avons besoin de calculer le cumul de résultats sur une certaine période. Nous avons une formule qui permet de calculer la sommes de termes consécutifs d’une suite $(v_n)$.
Définition 2.
Soit $(v_n)$ une suite géométrique de raison $q$ et de premier terme $v_0$. Alors, on appelle $S_n$ la somme des $n+1$ premiers termes consécutifs de la suite $(v_n)$. Alors, pour tout entier naturel $n$, $$S_n=v_0+v_1+v_2+\cdots+v_n$$ Donc, on peut écrire : $$S_n=v_0+v_0q^1+v_0q^2+\cdots+v_0q^n$$ ou encore : $$S_n=v_0(1+q+q^2+\cdots+q^n)$$
En effet, pour tout entier naturel $n$, la somme $S_n$ s’écrit : $$S_n=v_0+v_1+v_2+\cdots+v_n$$ Donc, pour tout entier naturel $n$ : $$S_n=v_0+v_0q^1+v_0q^2+\cdots+v_0q^n$$ Finalement, en mettant $v_0$ en facteur, on peut écrire : : $$S_n=v_0(1+q+q^2+\cdots+q^n)$$
Le $v_0$ devient un facteur multiplicateur de cette somme. Donc, on s’intéresse d’abord à la somme $$S’_n=1+q+q^2+\cdots+q^n$$
a) 1er cas : $v_0=1$ et $q=1$
Dans ce premier cas, la proposition suivante est évidente.
Proposition 2.
Pour tout entier naturel $n$ : $$S_n=1+1^1+1^2+\cdots+1^n=\text{nombre de termes}\quad(1)$$ Donc : $$\boxed{~S_n=1+1^1+1^2+\cdots+1^n=n+1~}\quad(2)$$
b) 2ème cas : $v_0=1$ et $q\not=1$
Propriété 4.
Soit $(v_n)$ une suite géométrique de raison $q$ et de premier terme $v_0=1$ et
$S’_n=1+q+q^2+q^3+\cdots+q^n$ la somme des $n+1$ premiers termes consécutifs de la suite, alors la somme $$\boxed{~S’_n=\dfrac{1-q^{\text{nombre de termes}}}{1-q}\quad(3)~}$$
Ici, nous avons donc : $$S’_n=\dfrac{1-q^{n+1}}{1-q}\quad(4)$$ ou encore $$S’_n=\dfrac{q^{n+1}-1}{q-1}\quad(4\,bis)$$
Remarque
1°) Le nombre de termes entre $v_0$ et $v_n$ est bien $=n-0+1=n+1$.
2°) En général, on utilise la formule (3) dans le cas où $0<q<1$ et la formule (4) dans le cas où $q>1$.
c) 3ème cas. Cas général $v_0\in\R$ et $q\not=1$
Propriété 5.
Soit $(v_n)$ une suite géométrique de raison $q$ et de premier terme $v_0\in\R$ et $S_n$ la somme des $n+1$ premiers termes consécutifs de la suite, alors la somme $S_n=v_0(1+q+q^2+\cdots+q^n)$. Alors :
$$\boxed{~S_n=v_0\times\dfrac{1-q^{\text{nombre de termes}}}{1-q}\quad(5)~}$$
Ici, nous avons donc : $$S_n=v_0\times\dfrac{1-q^{n+1}}{1-q}\quad(6)$$ ou encore $$S_n=v_0(1+q+q^2+q^3+\cdots+q^n)=v_0\times\dfrac{q^{n+1}-1}{q-1}\quad(5\,bis)$$
Exemple 3.
Soit $(v_n)$ une suite géométrique de raison $0,5$ et de premier terme $v_0=4$
1°) Calculer la somme $S_8=v_0+v_1+v_2+\cdots+v_8$.
2°) Calculer la somme $T_{8}=v_3+v_4+v_5+\cdots+v_{8}$.
