1. Probabilité théorique
Définitions 1.
Pour certaines expériences aléatoires, sous certaines conditions, on peut déterminer en pourcentage ou par un quotient « la chance » qu’un événement a pour se réaliser. Ce nombre s’appelle la « probabilité » ou « probabilité théorique » de l’événement.
Exemple 1.
Le lancer d’un dé à 6 faces parfaitement équilibré. On dit que le dé est non pipé ou non truqué. L’univers de l’expérience aléatoire est $\Omega=\{1;2;3;4;5;6\}$ ;
On peut supposer donc que les six faces ont exactement la même chance d’apparaître. Par conséquent, la probabilité théorique de l’apparition de chaque face est de $\dfrac{1}{6}$.
Si on note $E_1$= « obtenir la face $1$ », on a $E_1=\{1\}$ et $P(E_1) =\dfrac{1}{6}$.
On note de même $E_k$= « obtenir la face $k$ », $k=1;2;\ldots 6$, on a $E_k=\{k\}$ et $P(E_k) =\dfrac{1}{6}\simeq0,16666\ldots$.
On peut aussi écrire en langage symbolique : $P({\omega}) =\dfrac{1}{6}$ pour tout $\omega\in\Omega$.
De même, si $A$ = »le résultat est pair » alors $A=\{2 ; 4 ; 6\}$ et $A$ a trois chances sur six d’être réalisé. Donc $P(A) =\dfrac{3}{6}=\dfrac{1}{2}$ qu’on peut écrire $P(A) = 0,5$ ou encore $50\%$.
Remarque
La probabilité d’un événement est un nombre compris entre $0$ et $1$ qui s’écrit :
- sous la forme fractionnaire (numérateur inférieur au dénominateur) ;
- ou sous la forme d’un pourcentage (valeur arrondie en général) ;
- ou encore sous la forme d’un nombre décimale (valeur arrondie en général).
Exemple 2.
Une urne contient $10$ boules de même dimension et indiscernables au toucher, de couleur et numérotées : deux blanches $B_1$ et $B_2$ ; 3 rouges, $R_1$, $R_2$ et $R_3$ et 5 vertes $V_1$, $V_2$,$\ldots$, $V_5$. On tire une boule de cette urne et on note sa couleur et son numéro.
On peut supposer donc que les dix boules ont exactement la même chance d’être tirées. Par conséquent, la probabilité théorique du tirage de chaque boule est de \dfrac{1}{10} Si $R$ désigne l’événement « la boule tirée est rouge » alors $R=\{R_1;R_2;R_3\}$. Donc $P(R) =\dfrac{3}{10}$ qu’on peut écrire $P(R) = 0,3 =\dfrac{30}{100}$ donc $P(R) = 30\%$.
2. Probabilité et fréquence
Théorème 1. (Loi des grands nombres)
Si on répète une expérience aléatoire un très grand nombre de fois, les fréquences de réalisation de n’importe quel événement se rapprochent et finissent par se stabiliser autour de la probabilité théorique de l’événement.
Remarque
Si on lance un dé un certain nombre de fois (par exemple 10 fois ou 100 fois), même s’il est « parfaitement équilibré », nous ne sommes pas sûrs que chaque face aura « exactement » 1 chance sur 6 d’apparaître !
C’est pourquoi, nous parlons de « probabilité théorique » car, dans la pratique, les réalisations sont « aléatoires » donc imprévisibles. Mais le théorème nous affirme que, si on recommence un grand nombre de fois, nous nous approchons de cette probabilité théorique,…
3. Simulation de lancers d’un dé parfaitement équilibré.
Nous avons vu que, pour tout $\omega\in\Omega$, la probabilité théorique de chaque événement élémentaire est : $$P({\omega}) =\dfrac{1}{6}\simeq 0,16666\ldots$$
A l’aide d’un tableur, nous réalisons cette simulation en utilisant les fonctions ALEA.ENTRE.BORNES(- ; -) ou ALEA(), ENT(.) et NB.SI(- 😉.
Méthode
- Ouvrir un tableur EXCEL ou Libre Office CALC
- Entrer la formule dans la cellule A1 :
$\qquad\boxed{~\textbf{=ALEA.ENTRE.BORNES(1 ; 6)}~}$
$\qquad$ ou encore $\boxed{~\textbf{=ENT(6*ALEA()+1)}~}$. - Copier le contenu de la cellule A1 (avec la formule).
- Sélectionner une plage de la feuille du tableur en tapant A1:J10 dans la zone dédiée à cet effet. Ceci permet de sélectionner le rectangle ayant pour diagonale A1$\rightarrow$J10 comme indique ci-dessous.
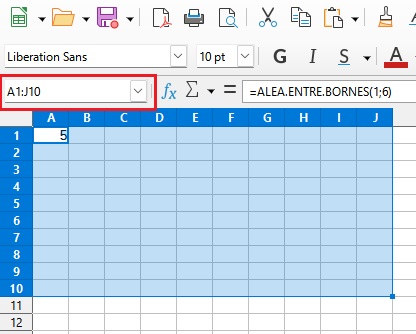
- Faites un clic-droit sur la zone sélectionnée, puis « Coller » le contenu de la cellule.
Nous obtenons maintenant 100 valeurs aléatoires entre 1 et 6 correspondant à la simulation de $100$ lancers d’un dé parfaitement équilibré.

Évidemment, nous pouvons recommencer la même procédure avec $1000$ valeurs (on arrondit au $1000$ème), puis $10\,000$, puis $100\,000$ valeurs, nous obtenons des fréquences très proches de $0,1666\ldots$
2.3, Calcul des probabilités
Définition 4.
Pour définir les probabilités des événements associés à une expérience aléatoire, on définit les probabilités de tous les événements élémentaires. On dit qu’on a donné la loi de probabilité de cette expérience.
Exemple 8.
La loi de probabilité du lancer d’un dé parfaitement équilibré est donnée par : pour tout $\omega\in\Omega$ : $P({\omega}) =\dfrac{1}{6}$. On peut aussi écrire la loi de probabilité dans un tableau :
$$\begin{array}{|c|c|c|c|c|c|c|c|}
\text{issues}~\omega &1&2&3&4&5&6&\text{Total}\\
P({\omega}) &\dfrac{1}{6}&\dfrac{1}{6}&\dfrac{1}{6}&\dfrac{1}{6}&\dfrac{1}{6}&\dfrac{1}{6}& 1\\
\end{array}$$
Théorème 2. (très important)
Dans une expérience aléatoire,
la probabilité $P(A)$ d’un événement $A$ est un nombre compris entre $0$ et $1$.. $$0\leqslant P(A)\leqslant $$
En particulier : $P(\emptyset)=0$ et $P({\Omega})=1$
la somme des probabilités de tous les événements élémentaires Ek ($1\leqslant k\leqslant n$) est égale à $1$ :
$$\text{Si}~\Omega=\{\omega_1 ; \omega_2 ; \omega_3 ;\ldots; \omega_n\},~\text{alors}~ P(E_1) + P(E_2) +\cdots+ P(E_n)=1$$
la probabilité d’un événement est égale à la somme des probabilités des événements élémentaires qui le constituent.
Exemple 9.
Un dé est truqué de telle façon que la probabilité de chaque face est proportionnelle au numéro de la face. Donner la loi de probabilité de cette expérience aléatoire.
On peut aussi écrire la loi de probabilité dans un tableau :
$$\begin{array}{|c|c|c|c|c|c|c|c|}
\text{Valeurs de}~\omega &1&2&3&4&5&6&\text{Total}\\
P({\omega})&a\times1 &a\times2 &a\times3 &a\times4 &a\times5&a\times6&1\\ \end{array}$$
D’après le théorème, la somme des probabilités de tous les événements élémentaires Ek est égale à 1. Donc : $P(E_1) + P(E_2) +\cdots+ P(E_6)=1$. Donc : $$a\times1+a\times2+\cdots+&a\times6=1$$ Donc $$a\times(1+2+3+4+5+6)=1$$
Ce qui donne : $$a\times21=1\quad\text{D’ou}\quad\boxed{~~a=\dfrac{1}{21}}$$
Par conséquent, la loi de probabilité de cette expérience aléatoire est donnée par le tableau suivant :
$$\begin{array}{|c|c|c|c|c|c|c|c|}
\text{Valeurs de}~\omega &1&2&3&4&5&6&\text{Total}\\
P({\omega}) &\dfrac{1}{21}&\dfrac{2}{21}&\dfrac{3}{21}&\dfrac{4}{21}&\dfrac{5}{21}&\dfrac{6}{21}& 1\\
\end{array}$$
Soit $A$ l’événement « le résultat est pair » ; alors $A=\{2 ; 4 ; 6\}$, donc : $$P(A)=\dfrac{2}{21}+\dfrac{4}{21}+\dfrac{6}{21}=\dfrac{12}{21}=\dfrac{4}{7}$$
2.4) Équiprobabilité
Définition 5.
Dans une expérience aléatoire, si tous les événements élémentaires ont la même probabilité d’être réalisés, on dit qu’on est dans une situation d’équiprobabilité ou que l’expérience aléatoire est équiprobable.
Exemple
Définition 6.
Si $A$ est un ensemble fini, on appelle cardinal de $A$, et on note $\card(A)$, le nombre d’éléments dans $A$.
Exemple 10.
Si $A$ désigne l’ensemble des nombres entiers pairs compris entre $1$ et $12$ (exclus), alors $A= \{2 ; 4 ; 6 ; 8 ; 10\}$ et $\card(A)=5$, puisque A contient $5$ éléments.
Théorème 3.
Dans une expérience aléatoire équiprobable ayant n événements élémentaires, on a :
la probabilité de chaque événement élémentaire est égale à $\dfrac{1}{n}$.
la probabilité d’un événement quelconque A est donnée par : $$\boxed{P(A)=\dfrac{\text{Nombre d’issues favorables}}{\text{Nombre d’issues possibles}}}$$
Exemple 11.
Tirage d’une carte dans un jeu de $52$ cartes (pas de joker).
Il y a $52$ issues possibles ;
L’univers $\Omega$ de l’expérience contient les $52$ cartes ;
Toutes les cartes ont la même chance d’être tirées. Donc, on est en situation d’équiprobabilité. La loi de probabilité de cette expérience est : $$\text{pour tout}\omega\in\Omega :\quad P({\omega}) =\dfrac{1}{52}$$
$A$ = « la carte tirée est un As » est un événement qui contient 4 issues favorables ; donc : $\card(A)= 4$ et $\card(\Omega) = 52$. Donc : $$P(A) =\dfrac{\card(A)}{\card(\Omega)}=\dfrac{4}{52}\quad\text{et}\quad P(A)=\dfrac{1}{13}$$
L’événement $T$ = « la carte tirée est un Trêfle » contient $13$ issues favorables.
$\card(T)= 13$ et $\card(\Omega) = 52$. Donc : $$P(T) =\dfrac{\card(T)}{\card(\Omega)}=\dfrac{13}{52}\quad\text{et}\quad P(A)=\dfrac{1}{4}$$
2.5. Événement contraire
Définition 5.
Dans une expérience aléatoire, on appelle événement contraire d’un événement A, l’événement, notéqui contient toutes les issues qui n’appartiennent pas à A.
Autrement dit : Pour tout $\omega\in\Omega$ : $\left[\omega\in\overline{A}\quad\text{(ssi)}\quad$\omega\not\in A\right]$
Exemple 12.
Une urne contient dix cartes identiques numérotées de $1$ à $10$. L’expérience aléatoire consiste à tirer une carte de cette urne. L’univers $\Omega$ est l’ensemble des nombres entiers de $1$ à $10$. Soit l’événement $A$ = »la carte tirée porte un numéro multiple de $3$ » donc : $A=\{3;6;9\}$. Donc $\card(A)= 3$ et $\card(\Omega) = 10$. Donc : $$P(A) =\dfrac{\card(A)}{\card(\Omega)}=\dfrac{3}{10}$$ On en déduit que : $\overline{A}=\{1 ; 2 ; 4 ; 5 ; 7 ; 8 ; 10\}$, $\card(\overline{A})= 7$ et $\card(\Omega) = 10$. Donc : $$P(\overline{A}) =\dfrac{\card(\overline{A})}{\card(\Omega)}=\dfrac{7}{10}$$
Remarque.
Si $A$ est un événement qui contient $p$ issues favorables (sur les n issues de $\Omega$), alors $\overline{A}$ contient $(n – p)$ issues favorables. Donc
$$P(\overline{A}) =\dfrac{\card(\overline{A})}{\card(\Omega)}=\dfrac{n-p}{n}=\dfrac{n}{n}-\dfrac{p}{n}=1-\dfrac{\card(A)}{\card(\Omega)}=1-P(A)$$
Théorème 4.
Dans une expérience aléatoire, si A est un événement et $\overline{A}$ son événement contraire, alors : $$\boxed{P(\overline{A}) =1-P(A)}$$
Exemple 13.
Dans l’exemple précédent, nous avons calculé $P(A)=\dfrac{3}{10}$ et $P(\overline{A})-\dfrac{7}{10}$. On aurait pu « déduire » directement ce dernier résultat du théorème 4, en écrivant : $$P(\overline{A})==1-P(A)=1-\dfrac{3}{10}=\dfrac{7}{10}$.
3. Probabilité de l’intersection ou réunion d’événements
3.1. Vocabulaire
Définitions 6.
Dans une expérience aléatoire, on consière deux événements $A$ et $B$.
$\quad$a) On appelle intersection des deux événements $A$ et $B$ et on note $A\cap B$, l’événement « $A$ et $B$ » qui est réalisé lorsque les deux événements $A$ et $B$ sont réalisés simultanément. Autrement dit : $A\cap B$ est réalisé si et seulement si, $A$ est réalisé et $B$ est réalisé.
$\quad$b) On appelle réunion des deux événements $A$ et $B$ et on note $A\cup B$, l’événement « $A$ ou $B$ » qui est réalisé lorsque l’un des deux événements $A$ ou $B$ est réalisé. Autrement dit : $A\cup B est réalisé si et seulement si, $A$ est réalisé ou $B$ est réalisé.
%==========================================
Figure intersection-Réunion
%==========================================
Définitions 7.
Dans une expérience aléatoire, on considère deux événements $A$ et $B$.
a) On dit que $A$ et $B$ sont deux événements incompatibles lorsque les deux événements $A$ et $B$ ne peuvent pas se réaliser simultanément. Autrement dit : $A$ et $B$ sont incompatibles si et seulement si, $A\cap B=\emptyset$.
Exemple 14.
Une urne contient dix cartes identiques numérotées de $1$ à $10$. L’expérience aléatoire consiste à tirer une carte de cette urne. L’univers $\Omega$ est l’ensemble des nombres entiers de $1$ à $10$. On considère les événements suivants :
- $A$ = »la carte tirée porte un numéro multiple de 3″, donc $A=\{ 3 ; 6 ; 9\}$ ;
- $B$ = »la carte tirée porte un numéro impair », donc $B$ = \{1; 3 ; 5 ; 7 ; 9\}$ ;
- $C$ = »la carte tirée porte un numéro multiple de 4″, donc $C=\{4 ; 8\}$.
$A\cap B$ = »$A$ et $B$ » = « la carte tirée porte un numéro impair et multiple de $3$ »
Donc $A\cap B=\{3 ; 9\}$. $A$ et $B$ ne sont pas incompatibles car $A\cap B\not=\emptyset$.
$A\cup B$= »$A$ ou $B$ » = « la carte tirée porte un numéro impair ou est multiple de $3$ ».
Donc $A\cup B=\{1; 3 ; 5 ; 6 ; 7 ; 9}$.
Par contre : $A\cap C$ = »$A$ et $C$ » = « la carte tirée porte un numéro multiple de $3$ et de $4$ »
Donc $A\cap C =\emptyset$. Donc $A$ et $C$ sont deux événements incompatibles.
Cas particulier.
Si $A$ est un événement, alors $A$ et $\overline{A}$ sont deux événements incomparibles.
3.2. Probabilité d’une réunion
Théorème 5.
Dans une expérience aléatoire, on considère deux événements A et B.
a) Si $A$ et $B$ sont deux événements quelconques, alors : $$ P(A\cup B) = P(A)+P(B)-P(A\cap B) $$
On peut en déduire immédiatement que : $$ P(A\cap B) = P(A)+P(B)-P(A\cup B) $$
b) Si $A$ et $B$ sont incompatibles, alors : $$ P(A\cup B) = P(A)+P(B)$$
%======================================
Figure ?
%======================================
Démonstration.
a) Pour démontrer ce résultat, il suffit de dénombrer (compter) les nombres d’élements dans chaque ensemble.
Dans $A\cup B$, si on additionne le nombre d’éléments de $A$ et le nombre d’éléments de $B$, on aura compté 2 fois le nombre d’éléments de $A\cap B$. Donc, il faut le soustraire une fois. Ce qui donne :
$$\card(A\cup B) = \card(A) + \card(B)-\card(A\cap B)$$
En divisant les deux membres par $\card(\Omega) = n$, on obtient : $$P(A\cup B)=\dfrac{\card(A)}{n}+\dfrac{\card(B)}{n}-\dfrac{\card(A\cap B)}{n}$$
D’où le résultat : $$P(A\cup B) = P(A) + P(B) – P(A\cap B) $$
b) Ce deuxième résultat est un cas particulier du a). En effet, si $A$ et $B$ sont incompatibles, alors $A\cap B=\emptyset$. Comme $P(A\cap B)=P(\emptyset) = 0$. D’où le résultat. CQFD.
Exemple 14.
Dans une classe de Seconde de $35$ élèves, option langues vivantes, $5$ élèves font uniquement du russe, et parmi les trente autres, vingt font anglais et dix-huit font espagnol. On choisit au hasard un élève dans cette classe. Calculer les probabilités de
$R$ = « l’élève fait du russe », $A$ = « l’élève fait de l’anglais », $E$ = « l’élève fait de l’espagnol », $F$ = « l’élève fait du russe et de l’anglais » et $G$ = »l’élève fait de l’anglais et de l’espagnol ».
$\Omega$ est l’ensemble des trente-cinq élèves. On est dans une situation d’équiprobabilité.
a) $$P(R)=\dfrac{\card(R)}{\card(\Omega)}=\dfrac{5}{35}=\dfrac{1}{7}$$
$$P(A)=\dfrac{\card(A)}{\card(\Omega)}=\dfrac{20}{35}=\dfrac{4}{7}$$
et $$P(E)=\dfrac{18}{35}$$
b) Il n’y a aucun élèves qui fait à la fois russe et anglais. Donc, les deux événements $R$ et $A$ sont incompatibles. Donc $P(R\cap A)=P(\emptyset) = 0$.
c) D’après l’énoncé, $30$ élèves font « Anglais ou Espagnol ». Donc $\card(A\cup E )=30$.
$$P(A\cup E )=\dfrac{\card(A\cup E )}{\card(\Omega)}=\dfrac{30}{35}=\dfrac{6}{7}$$
Or, d’après le théorèmee 5, on a : $$P(A\cup E )=P(A)+P(E )-P(A\cap E )$.
En rempalçant par les valeurs connues, on obtient : $$\dfrac{6}{7}=\dfrac{6}{7}+\dfrac{18}{35}-P(A\cap E )$$
Donc : $$P(A\cap E )=\dfrac{20}{35}+\dfrac{18}{35}-\dfrac{30}{35}
D’où : $$: $$P(A\cap E )=\dfrac{8}{35}$$
Conclusion : $8$ élèves sur les $35$ font « anglais et espagnol ».
4. Utiliser un arbre pour calculer des probabilités
Dénombrer toutes les issues possibles
Exemple 15.
Une famille a deux enfants. On suppose qu’il y a autant de chances d’obtenir un garçon qu’une fille. Calculer la probabilité des événements « obtenir deux filles » puis « obtenir deux enfants de sexes différents ». (On suppose qu’il n’y a pas de jumeaux).
On appelle $F$ l’événement « obtenir une fille » et $G$ l’événement « obtenir un garçon » à chaque naissance :
1er enfant 2ème enfant issues possibles
Un arbre permet de distinguer tous les cas possibles, donc toutes les issues possibles.
Une branche = Un cas
%====================================
Figure arbre de dénobrement
%====================================
L’univers associé à cette situation comporte quatre issues possibles. Donc :
W = {FF ; FG ; GF ; GG }. Ainsi, La probabilité d’obtenir deux filles est :
$$P(\text{« FF »}) =\dfrac{\text{Nombre d’issues favorables}}{\text{Nombre d’issues possibles}}=\dfrac{1}{4}$$
et si on appelle $B$ = « obtenir deux enfants de sexes différents », on a $B=\{FG ; GF\}$ et $\card(B) = 2$.
Donc $P(B) =\dfrac{2}{4}=\dfrac{1}{2}$.
Remarque : Pour trois enfants, faites un arbre et montrer qu’il y a 8 issues possibles !
Arbre pondéré pour calculer des probabilités
Définitions 8.
Dans une expérience aléatoire, on consière deux événements $A$ et $B$.
On dit qu’un arbre est pondéré lorsque, sur chaque branche, on indique la probabilité d’obtenir l’événement suivant.
Théorème. Règles de calcul avec un arbre pondéré
Règle 1 : La somme des probabilités des branches partant d’une même racine est toujours égale à 1 :
Règle 2 : La probabilité d’un chemin est égale au produit des probabilités des branches de ce chemin.
Règle 3 : La probabilité d’un événement est la somme des probabilités des chemins correspondant à cet événement.
Exemple 16.
On lance un dé parfaitement équilibré. On note la face obtenue. On recommence l’épreuve 1 fois. Calculer la probabilité de des événements suivants :
$E$ = « N’obtenir aucun $5$ sur les deux lancers » et $F$ = « Obtenir exactement un sel $5$ ».
Pour chaque lancer, il n’y a que deux issues possibles : $C$ = « obtenir un $5$ » et $\overline{C}$ = « obtenir un nombre autre que $5$ ».
Donc, d’après ce qui précède $\Omega =\{CC ; C\overline{C}; \overline{C}C;\overline{C}\overline{C}\}$.
Le dé est parfaitement équilibré, donc chaque lancer est une expérience équiprobable Donc : $P(C) =\dfrac{1}{6}$ et $P(\overline{C})=1-P(C)=1-\dfrac{1}{6}=\dfrac{5}{6}$.
1er lancer 2ème lancer Probabilité de chaque chemin
%========================================
Figure arbre pondéré
%========================================
$E$ = « $\overline{C}\overline{C}$ » = chemin bleu ; $F$ = »C\overline{C} » = la somme des 2 chemins rouges :
$P(E)=P(« \overline{C}\overline{C} ») =\dfrac{25}{36}$ et $P(F)=P(« C\overline{C} ») + P(« \overline{C}C ») = \dfrac{5}{36}\dfrac{5}{36}=\dfrac{10}{36}$.
