Dans toute le chapitre sur la géométrie dans l’espace, la figure de référence est le cube. Un cube $ABCDEFGH$ permet de réaliser des constructions du parallélisme, de l’orthogonalité et permet également de définir un repère dans l’espace pour écrire les expressions analytiques (avec les coordonnées) de points, de vecteurs, de droites et de plans, etc.

1. Positions relatives de droites dans l’espace

Définitions 1.
On distingue deux cas :
1°) On dit que deux droites sont coplanaires, lorsqu’elles sont contenues dans un même plan. Elles peuvent donc être sécantes, parallèles ou confondues.
2°) On dit que deux droites sont non coplanaires, lorsqu’elles ne sont pas contenues dans un même plan.

Exemples
ABCDEFGH est un cube. Figure 1.

Figure 1.
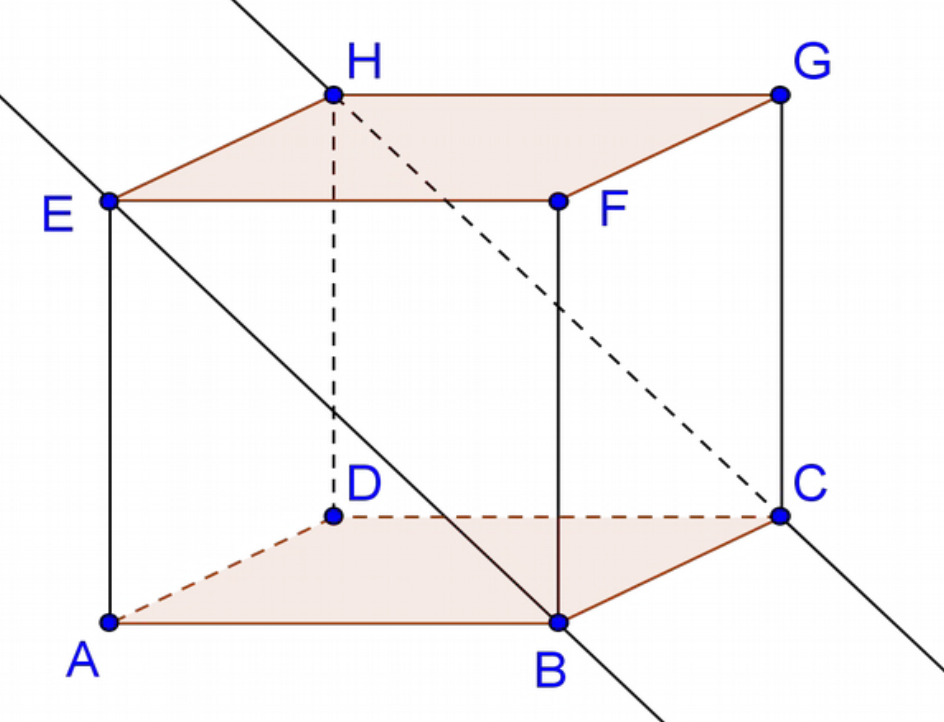
  • Les droites $(AC)$ et $(BE)$ ne sont pas coplanaires.
  • Les droites $(BE)$ et $(HC)$ sont parallèles.
  • Les doites $(AG)$ et $(EC)$ sont sécantes.
  • Les doites $(BF)$ et $(HC)$ ne sont pas coplanaires.
  • Les droites $(AH)$ et $(BG)$ sont parallèles.
  • Les doites $(EG)$ et $(BG)$ sont sécantes.

2. Positions relatives d’une droite et d’un plan dans l’espace

Propriété n°1.
Une droite $d$ est parallèle à un plan $P$ si elle est parallèle à une droite d’contenue dans le plan $P$.

Soit $d$ une droite et $P$ un plan dans l’espace. On distingue trois cas :

Figure 2.
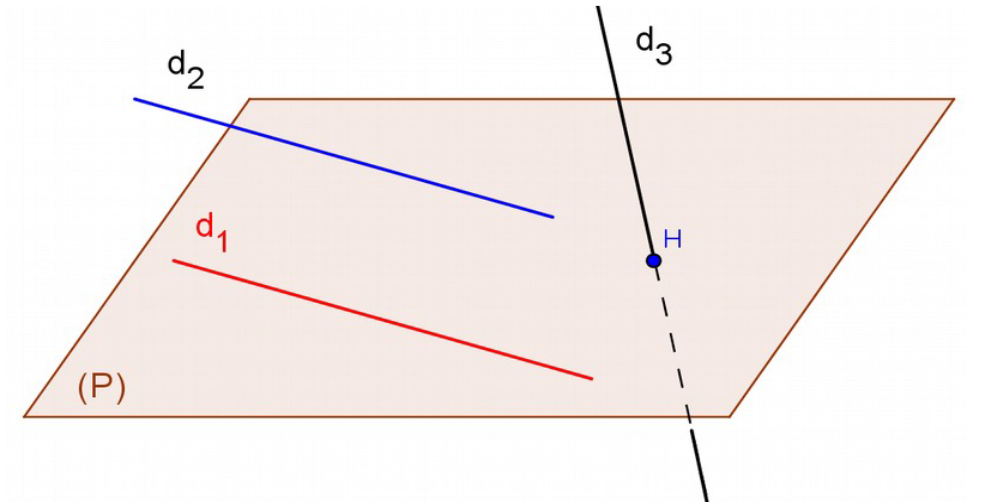
$d_1\subset P$ donc $d_1//P$.
$d_2//d_1$ et $d_1\subset P$ donc $d_2//P$ et $d_2\cap P=\emptyset$
$d_3\cap P=\{H\}$, donc $d_3//\!\!\!\!\!\diagdown P$

– La droite $d_1$ est [entièrement] contenue dans le plan $P$, donc tous les points de $d_1$ appartiennent aussi au plan $P$ ;
– La droite $d_2$ est strictement parallèle au plan $P$, donc $d_2$ et $P$ n’ont aucun point commun ;
– La droite $d_3$ est sécante au plan $P$, donc $d_3$ et $P$ ont un seul point commun, le point $H$.

3. Positions relatives de deux plans dans l’espace

Définition 2.
Trois points non alignés $A$, $B$ et $C$ de l’espace définissent un plan et un seul, noté $(ABC)$.

Soit $P_1$ et $P_2$ deux plans dans l’espace. On distingue trois cas :

$\bullet$ 1er cas : Les deux plans $P_1$ et $P_2$ sont confondus. Donc $P_1=P_2$. Donc, on a aussi $P_1//P_2$ et $$\boxed{~P_1\cap P_2=P_1=P_2~}$$

Figure 3. $P_1=P_2$

$\bullet$ 2ème cas : les deux plans $P_1$ et $P_2$ sont strictement parallèles, donc $P_1$ et $P_2$ n’ont aucun point commun et $$\boxed{~P_1//P_2 ~~\text{et}~~P_1\cap P_2=\emptyset~}$$

Figure 4.
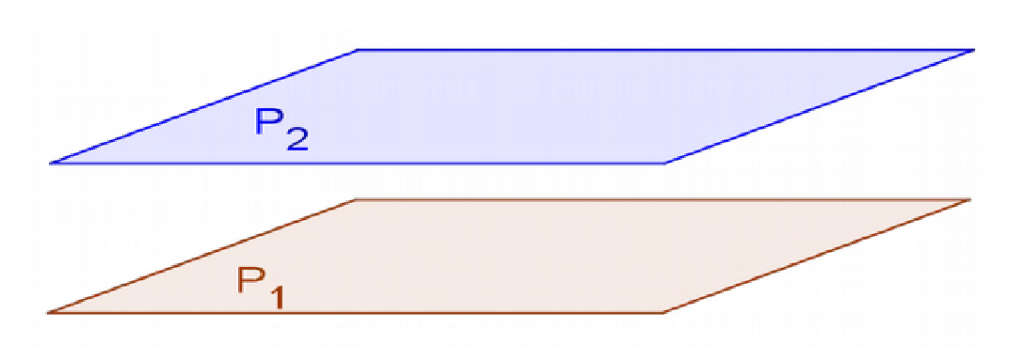
$P_1//P_2~~\text{et}~~P_1\cap P_2=\emptyset$

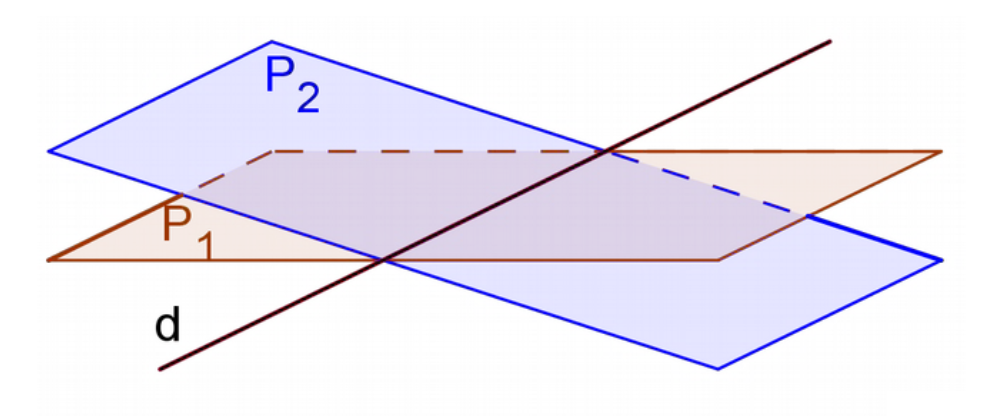
$\bullet$ 3ème cas : les deux plans $P_1$ et $P_2$ sont sécants et leur intersection est une droite $d$ : $$\boxed{~P_1//\!\!\!\!\!\diagdown P_2 ~~\text{et}~~P_1\cap P_2=d~}$$

Figure 5. $P_1//\!\!\!\!\!\diagdown P_2$ et $P_1\cap P_2=d$.

4. Exercices résolus

Exercice résolu n° 1.
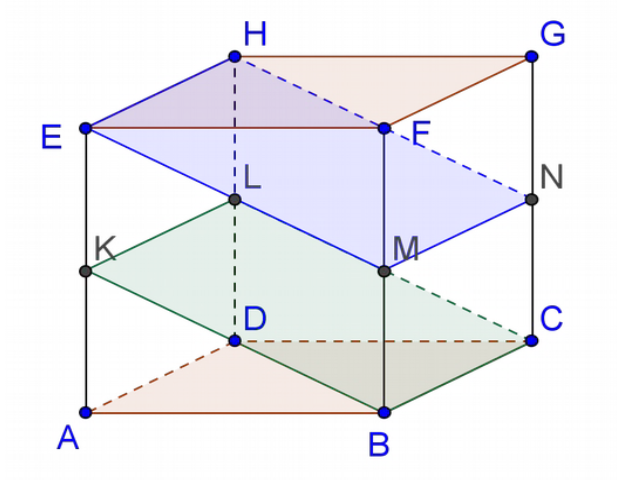
$ABCDEFGH$ est un cube. Les points $K$, $L$, $M$ et $N$ sont les milieux respectifs des arêtes $[AE]$, $[DH]$, $[BF]$ et $[CG]$. Dire si les affirmations suivantes sont vraies ou fausses et justifiez votre réponse.
(1) Les plans $(BKC)$ et $(CDG)$ sont sécants.
(2) La droite $(AC)$ est sécante au plan $(BKC)$.
(3) La droite $(BK)$ est sécante au plan $(ADC)$.
(4) Les plans $(BKC)$ et $(EMN)$ sont parallèles.

Figure 6. Le cube $ABCDEFGH$.


CQFD. $\blacktriangle$

Exercice résolu n° 2.


CQFD. $\blacktriangle$