Dans toute le chapitre sur la géométrie dans l’espace, la figure de référence est le cube. Un cube $ABCDEFGH$ permet de réaliser des constructions du parallélisme, de l’orthogonalité et permet également de définir un repère dans l’espace pour écrire les expressions analytiques (avec les coordonnées) de points, de vecteurs, de droites et de plans, etc.

Ortho (en grec) = « droit » et gonia (en grec) = « angle ».
On retrouve le mot dans ortho dans (repère) ortho-gonal, mais aussi dans poly-gone. Ainsi par exemple, un polygone à dix côtés, mais aussi dix angles et s’appelle un décagone.

1. Orthogonalité de deux droites dans l’espace

Définition 1. (Rappel)
On dit que deux droites sont perpendiculaires si et seulement si elles sont sécantes (donc coplanaires) et forment un angle droit.

Définition 2.
Soient $d_1$ et $d_2$ deux droites dans l’espace et $A\in d_1$.
On dit que les droites $d_1$ et $d_2$ sont orthogonales si $d_1$ est perpendiculaire à une droite $d’_2$, parallèle à $d_2$ et passant par $A$.
Autrement dit :
Deux droites $d_1$ et $d_2$ sont orthogonales si leurs parallèles passant par un point donné sont perpendiculaires.

Figure 1.

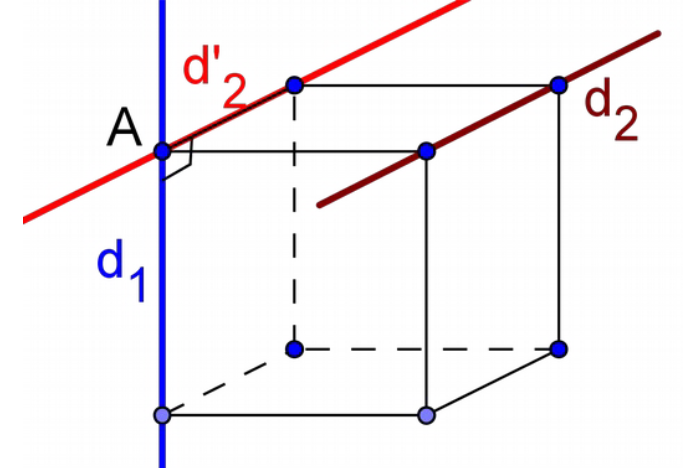
Exemples

Figure 2.

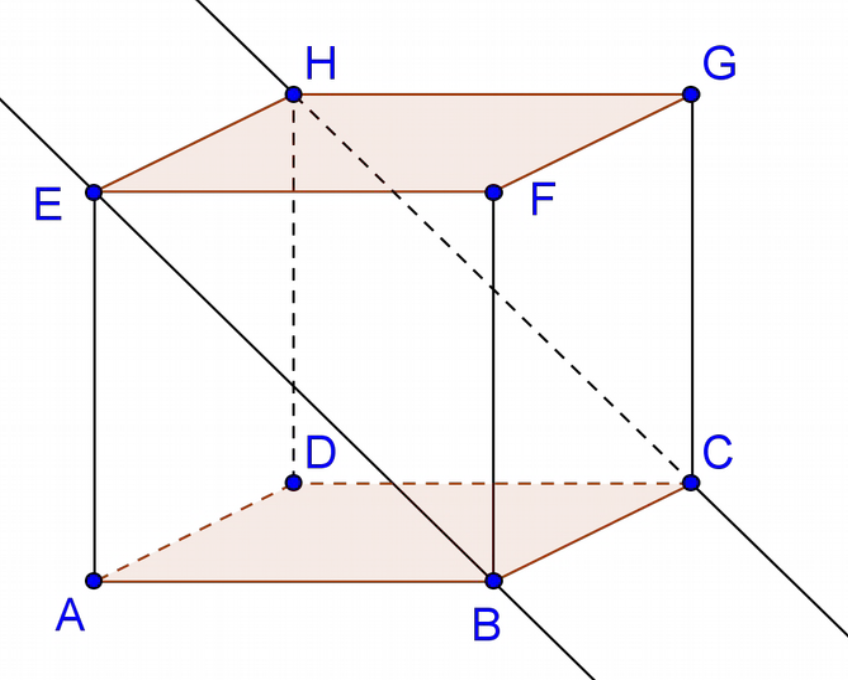
Exercice résolu n°1.
$ABCDEFGH$ est un cube.
1°) Les droites $(AG)$ et $(CE)$ sont-elles orthogonales ?
2°) Les droites $(AC)$ et $(BF)$ sont-elles orthogonales ?
3°) Les droites $(AD)$ et $(BE)$ sont-elles orthogonales ?

1°) NON. Les droites $(AG)$ et $(CE)$ ne sont pas orthogonales ; car elles sont contenues dans le plan $(ACE)$ et sont les diagonales du rectangle $ACGE$ qui n’est pas un carré.

2°) OUI. Les droites $(AC)$ et $(BF)$ sont orthogonales ; car $(AC)$ perpendiculaire à $(CG)$ et $(BF)//(CG)$.

3°) OUI. Les droites $(AD)$ et $(BE)$ sont orthogonales ; car $(AD)//(BC)$ et $(BC)$ est perpendiculaire à $(BE)$.
CQFD. $\blacktriangle$

Propriété n°1.
($P_1$) Si deux droites sont parallèles, toute droite orthogonale à l’une est orthogonale à
l’autre.

Cette propriété est naturellement fausse si on remplace « orthogonale » par « perpendiculaire ».

2. Orthogonalité d’une droite et d’un plan dans l’espace

Définition 3. (Rappel)
Une droite est perpendiculaire à un plan si et seulement si elle est perpendiculaire à deux droites sécantes contenues dans ce plan.

Figure 3.

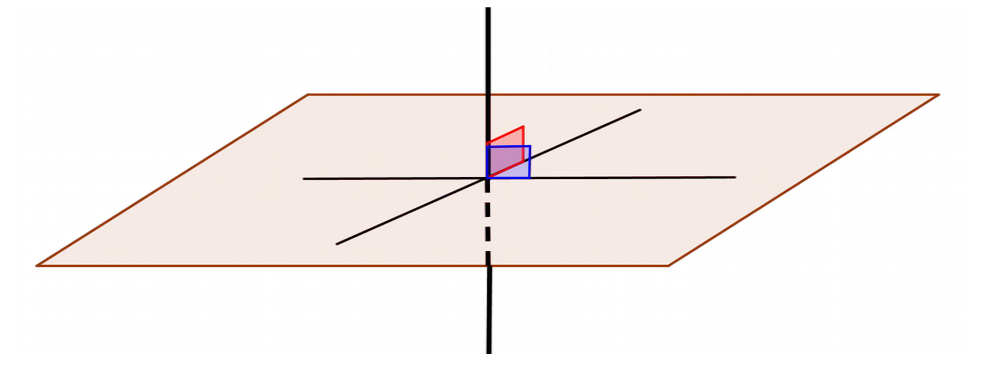
Définition 4.
Une droite est orthogonale à un plan si et seulement si elle est orthogonale à deux droites sécantes contenues dans ce plan.

Propriété n°2.
($P_2)$ Une droite est orthogonale à un plan si et seulement si elle est orthogonale à toutes les droites contenues dans ce plan.

Exemples

$ABCDEFGH$ est un cube. (Figure 4.) La droite $(AB)$ est orthogonale à la droite $(FC)$.

Figure 4.

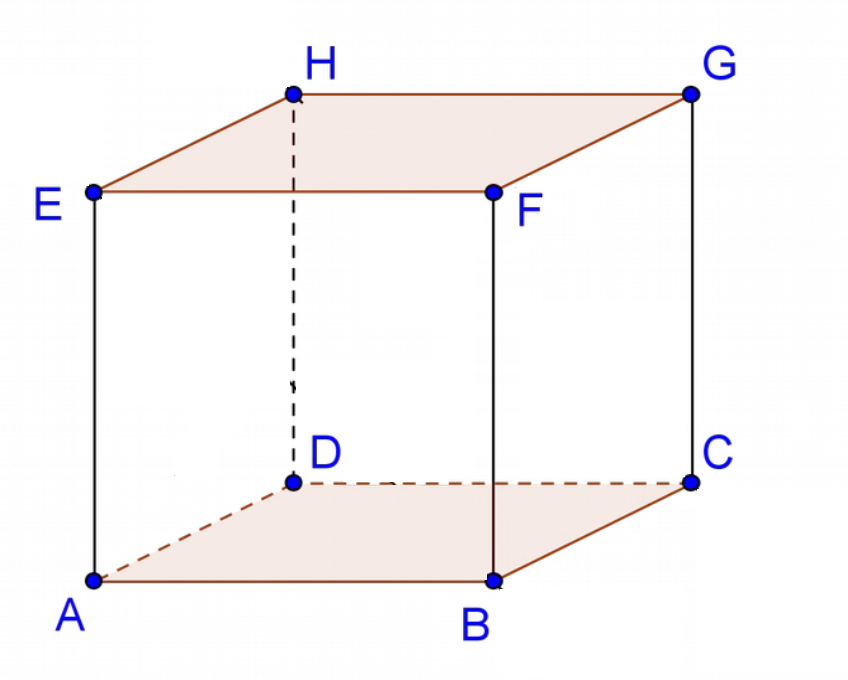
En effet, la droite $(AB)$ est perpendiculaire aux deux droites $(BF)$ et $(BC)$ contenues dans le plan $(BFC)$. Donc, la droite $(AB)$ est orthogonale au plan $(BFC)$.
Par conséquent, la droite $(AB)$ est orthogonale à toute droite contenue dans le plan $(BFC)$. En particulier, la droite $(AB)$ est orthogonale à la doite $(FC)$.

3. Propriétés de l’orthogonalité

On peut reprendre toutes les propriétés vues au collège sur les droites et remplacer « perpendiculaire » par « orthogonale » puis analyser toutes les « combinaisons » possibles entre droites, entre plans et entre droites et plans dans l’espace. Nous allons découvrir que certaines propriétés, valables pour « droites perpendiculaire » en géométrie plane, ne le seront plus dans l’espace. Cependant, si on remplace « perpendiculaire » par « orthogonale », certaines propriétés deviennent vraies dans l’espace.

Propriétés
($P_3$) Si deux droites sont orthogonales à un même plan, alors elles sont parallèles.

($P_4$) Si deux droites sont parallèles, alors tout plan orthogonal à l’une est orthogonal à l’autre.

($P_5$) Si deux plans sont parallèles, alors toute droite orthogonale à l’un est orthogonale à l’autre.

($P_6$) Si deux plans sont orthogonaux à une même droite, alors ils sont parallèles.

Le théorème du toit (ROC).

Figure 7.

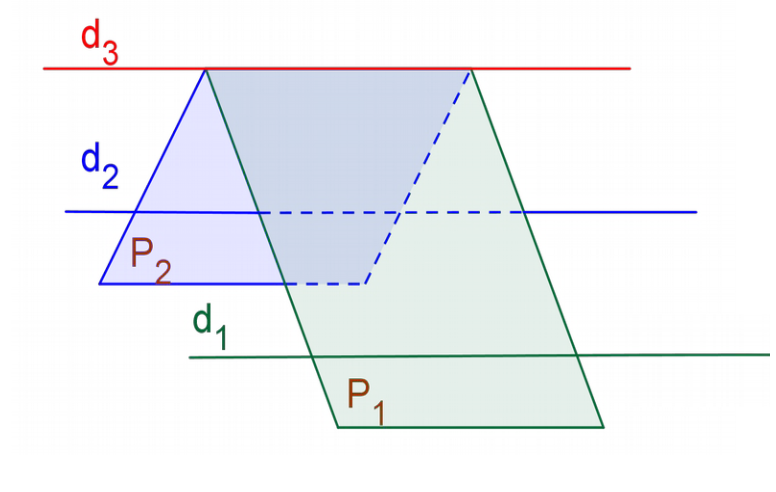
($P_7$) Soit $P_1$ et $P_2$ deux plans sécants contenant deux droites parallèles $d_1$ et $d_2$ respectivement. Alors l’intersection de $P_1$ et $P_2$ est une droite $d_3$ parallèle à $d_1$ et $d_2$.

Par hypothèse, les plans $P_1$ et $P_2$ sont sécants, on appelle $d_3$ la droite intersection des plans $P_1$ et $P_2$.
Les droites $d_1$ et $d_2$ sont parallèles. Donc : $$P_1\cap P_2 = d_3~~\text{et}~~d_1//d_2$$
Les droites $d_1$ et $d_2$ sont parallèles donc elles sont coplanaires.
Donc, il existe un plan $P_3$ qui contient à la fois $d_1$ et $d_2$.
Mais alors, $d_1$ et $d_3$ sont contenues dans $P_1$ ; et $d_2$ et $d_3$ sont contenues dans $P_2$. Donc : $$P_1\cap P_3=d_1~~\text{et}~~P_2\cap P_3=d_2$$

Montrons que $d_1//d_3$.
Supposons que $d_1$ et $d_3$ ne soient pas parallèles. Donc elles sont sécantes en un point $A$.

$\bullet$ Comme $A\in d_1\cap d_3$ donc $A\in d_1$ et $A\in d_3$.
Or, $d_3=P_1\cap P_2$ et $A\in d_3$, on peut affirmer que $A\in P_2$.
Ce qui donne : $A\in P_2\cap P_3$. Or, $P_2\cap P_3=d_2$. Par conséquent : $\boxed{~A\in d_2~}$. Et comme $A\in d_1$, on en déduit que $d_1$ et $d_2$ sont sécantes en $A$. Ce qui est absurde, contraire à notre hypothèse.

Par conséquent les droites $d_1$ et $d_3$ sont parallèles.
Or, par hypothèse : $d_1$ et $d_2$ sont parallèles, on en déduit que les droites $d_2$ et $d_3$ sont aussi parallèles.

Conclusion : L’intersection de $P_1$ et $P_2$ est une droite $d_3$ parallèle à la fois à $d_1$ et $d_2$. CQFD. $\blacktriangle$

Exercice résolu n°2.
$ABCDEFGH$ est un cube.


CQFD. $\blacktriangle$