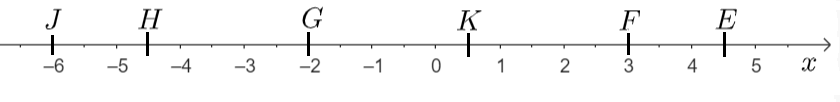1. Activité
Exercice résolu.
Dans le tableau suivant, on donne les températures à 9h et à 16h des 8 villes A, B, C, D, E, F, G et H. $$\begin{array}{|l|c|c|c|c|c|c|c|c|}\hline
\text{Villes} & A& B& C& D& E& F& G&H \\ \hline
\text{Temp. à 9h}& 12^\circ&14^\circ&10^\circ&17^\circ&8^\circ&21^\circ&14^\circ&6^\circ \\ \hline
\text{Temp. à 16h}& 16^\circ&11^\circ&10^\circ&13^\circ&10^\circ&28^\circ&9^\circ&0^\circ \\ \hline
\text{Variation} &\cdots &\cdots &\cdots &\cdots &\cdots &\cdots &\cdots &\cdots \\ \hline
\end{array}$$
1°) Recopier et compléter par un nombre relatif, la variation de température entre 9h et 16h dans chaque ville.
2°) Quelles sont les villes où la température a augmenté ? Comme les reconnaît-on ?
3°) Quelles sont les villes où la température a baissé ? Comme les reconnaît-on ?
4°) Que se passe-t-il dans la ville C ?
2. Les Nombres relatifs
Définitions 1.
On distingue trois types de nombres relatifs :
$\bullet$ Un nombre précédé ou non d’un signe $+$ est un nombre positif.
$\bullet$ Un nombre précédé d’un signe $-$ est un nombre négatif.
$\bullet$ Le nombre $0$ est à la fois un nombre positif et un nombre négatif. On dit que $0$ est le nombre nul. $+0=-0=0$.
Les nombres positifs, négatifs ou nuls s’appellent les nombres relatifs.
Notations
Dans un premier temps, les nombres relatifs sont notés entre parenthèses précédés de leurs signes. Exemple : $(+4,5)$ ou $(-3,25)$, etc.
Un nombre positif peut s’écrire avec ou non le signe $+$. Par exemple, $(+5,3)$ s’écrit aussi $+5,3$ ou encore $5,3$. $$\boxed{~(+5,3)=+5,3=5,3~}$$
Exemples
$5,3$ ; $(+2,05)$ ; $+12$ ; $0,7$ et $0$ sont des nombres relatifs.
En particulier $-5,3$ et $+5,3$ sont des nombres relatifs opposés.
3. Droite graduée
Définitions 2.
Soit $d$ une droite dans le plan.
On définit une graduation sur la droite $d$ en se donnant 2 points et un sens :
$\bullet$ Le point $O$ est l’origine de la graduation, son abscisse est zéro ; $x_O=0$.
$\bullet$ Le point $I$ est le point unité. La longueur $OI$ est l’unité de la graduation.
On a : $OI=1$. L’abscisse du point $I$ est égal à $+1$.
$\bullet$ Le sens croissant est le sens qui va de $O$ vers $I$.
Propriété 1.
Tout point $M$ de la droite graduée $d$ est repéré par un nombre relatif qu’on note $x_M$ (Lire $xM$ ou $x$ indice $M$) et qu’on appelle l’abscisse du point $M$.
« abscisse » est un mot féminin. On dit : « une abscisse ».
Un « indice » sert à « indiquer ».
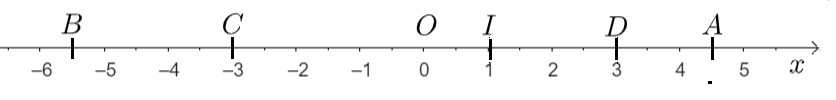
Exemples
L’abscisse du point $A$ est $(+4,5)$ ; l’abscisse du point $B$ est $(-5,5)$. Le pont $C$ a pour abscisse $(-3)$ et $D$ a pour abscisse $(+3)$. Les abscisses des points $C$ et $D$ sont opposées. Le point $O$ est donc le milieu du segment $[CD]$.
On écrit :
$x_A=(+4,5)$ ou $A(+4,5)$.
$x_B=(-5,5)$ ou $B(-5,5)$.
$x_C=(-3)$ ou $C(-3)$.
$x_D=(+3)$ ou $D(+3)$.
$x_O=0$ ou $O(0)$.
$x_I=(+1)$ ou $I(+1)$.
4. Partie numérique ou Distance à zéro
Propriété 2 (et définition)
Tout nombre relatif est entièrement déterminé par la donnée par :
$\bullet$ un signe $(+)$ ou $(-)$
$\bullet$ une partie numérique appelée aussi valeur absolue ou distance à zéro et qu’on désigne entre 2 barres.
Exemples
$x_A=(+4,5)$ donc la distance à zéro de $(+4,5)$ est $|+4,5| = 4,5$.
$x_B=(-5,5)$ donc la distance à zéro de $(-5,5)$ est $|-5,5| = 5,5$.
$x_C=(-3)$ donc la distance à zéro de $(-3)$ est $|-3| = 3$.
$x_D=(+3)$ donc la distance à zéro de $(+3)$ est $|+3| = 3$.
$x_O=0$ donc la distance à zéro de $0$ est $|0| = 0$.
$x_I=(+1)$ donc la distance à zéro de $(+1)$ est $|+1| = 1$.
5. Exercices résolus
Exercice n°2.
Tracer une droite graduée $(OI)$ avec une unité $OI=1$cm.
Placer les points $E(+4,5)$, $F(+3)$, $G(-2)$, $H(-4,5)$, $J(-6)$ et $K(+0,5)$.
On regarde d’abord les points le plus loin de $0$, du côté des nombres négatifs et du côté des nombres positifs. Ici $J$ est à 6 unités à gauche et $E$ est à 4,5 unités à droite. Puis je place les points avec leurs abscisses.
Exercice n°3.
Déterminer les parties numériques (ou distances à zéro) des nombres relatifs suivants :
$(+4,5)$, $(+3)$, $(-2)$, $(-4,5)$, $(-6)$ et $(0,5)$.