La démonstration en Géométrie au collège

La démonstration en géométrie au collège repose sur quelques idées simples que les élèves doivent apprendre à maîtriser progressivement.

Ainsi, la démonstration est un raisonnement, c’est-à-dire un enchaînement logique, qui permet de montrer qu’une affirmation géométrique est vraie. Elle s’appuie toujours sur des informations données dans l’énoncé, sur des propriétés connues et une progression logique.

On commence par faire une figure, à main levée si ce n’est pas demandé, pour fixer les idées.
Puis, on doit rappeler ce que l’on sait : cela peut être une donnée de la figure, une mesure, une égalité de segments, une parallèle, un angle droit, ou une construction.
Ensuite, on utilise des propriétés connues, par exemple celles des triangles, des angles, des parallélogrammes ou des perpendiculaires. Et enfin, l’idée est de relier les informations entre elles pour arriver à la conclusion demandée.

Une démonstration en géométrie fonctionne un peu comme une histoire dont chaque phrase découle de la précédente. Évidemment, on ne saute pas d’étapes et on ne se contente pas de regarder la figure. Par conséquent, on doit justifier toujours avec une propriété ou un théorème. C’est cela qui montre que la conclusion ne dépend pas de la construction de la figure, mais de la logique utilisée.

Dans les classes de collège, les démonstrations utilisent souvent les mêmes types de propriétés. Par exemple, si deux angles sont alternes-internes et que les droites sont parallèles, on peut affirmer qu’ils sont de même mesure. Si deux côtés d’un triangle sont de même longueur, alors ce triangle est isocèle, donc on sait que les angles à la base sont de même mesure. Si un quadrilatère a ses côtés opposés parallèles, on sait que c’est un parallélogramme. En plus, ces règles permettent d’avancer pas à pas vers la conclusion attendue.

Pour aider les élèves, on peut proposer une structure simple en trois étapes : d’abord écrire ce qui est donné, ensuite expliquer ce que l’on en déduit grâce aux propriétés connues, et enfin formuler clairement la conclusion. Avec l’habitude, la démarche devient plus naturelle et on gagne en précision et en rigueur dans le raisonnement.

1. Étude d’un exemple

Exercice résolu n°1.
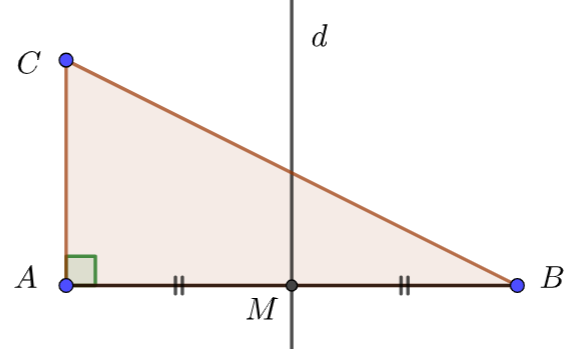
$ABC$ est un triangle rectangle en $A$. Par le milieu $M$ du côté $[AB]$, on trace la
droite $d$ parallèle à $(AC)$.
Démontrer que la droite $d$ est la médiatrice du segment $[AB]$.

2. La structure classique d’une démonstration

a) Premier réflexe : Faire une figure et la coder pour illustrer le problème (même à main levée propre).

« Une figure bien faite et bien codée est un problème à moitié résolu » Albert EINSTEIN.

b) Deuxième réflexe : Écrire les hypothèses : Ce sont les informations données
(on dit simplement « les données » du problème). A souligner dans l’énoncé !

Exemple : $ABC$ est un triangle rectangle en $A$. Par le milieu $M$ du côté $[AB]$, on trace la droite $d$ parallèle à $(AC)$. Démontrer que la droite d est la médiatrice du segment $[AB]$.

(H1) : Le triangle $ABC$ est rectangle en $A$ ;
(H2) : Le point $M$ est le milieu du segment $[AB]$ ;
(H3) : $M\in d$ ; (ce n’est pas dit directement !)
(H4) : $d // (AC)$.

c) Troisième réflexe : Écrire ce qu’on doit démontrer, en disant « Montrons que… ».
Ici, Montrons que « $d$ est la médiatrice du segment $[AB]$ ».

d) Quatrième réflexe : Réfléchir aux propriétés qu’on peut utiliser, en lien avec les hypothèses et la conclusion.
Je dois immédiatement penser à (1) la définition de la médiatrice et (2) à la propriété caractéristique de la médiatrice.

2.2. Méthode de rédaction d’une démonstration « On sais que…, Or…, Donc… »

— « On sais que » et je cite l’hypothèse utilisée,
— « Or » et je (ré)cite la propriété ou le nom du théorème …
— « Donc » et j’écris la conclusion…

2.3. La démonstration de l’exercice

Par hypothèse, on sait que d passe par le milieu $M$ du segment $[AB]$.
On sait aussi que $ABC$ est un triangle rectangle en $A$, donc les droites $(AB)$ et $(AC)$ sont
perpendiculaires. Donc : $$(AB)\perp(AC)$$
De plus, on sait que $d // (AC)$.
Or, d’après la propriété qui dit que : « Si deux droites sont parallèles, toute droite perpendiculaire à l’une est perpendiculaire à l’autre », on peut affirmer que les droites $(AB)$ et $d$ sont perpendiculaires. Donc : $$d\perp(AB)$$
Par conséquent, la droite $d$ est perpendiculaire au segment $[AB]$ et passe par son milieu.

Conclusion. La droite $d$ est la médiatrice du segment $[AB]$.
CQFD (Ce qu’il fallait démontrer !)

3. La démonstration

3.1. La méthode

1. Faire une figure et bien la coder pour illustrer le problème ;
2. Écrire les hypothèses et ce qu’on doit démontrer ;
3. Bien observer la figure et chercher des pistes… ;
4. Faire des liens avec les règles et propriétés connues ;
5. Tirer des conséquences directes des hypothèses ;
6. Ordonner et enchaîner les idées ;
7. Enfin, rédiger la démonstration.

3.2. La rédaction

• Faire un raisonnement logique
• Raisonner = argumenter = justifier
• Démontrer = prouver = justifier
• Déduire = extraire une information = tirer une conséquence des données précédentes

Chaque déduction est une conséquence d’une ou plusieurs hypothèses en utilisant une propriété. On dit : « On sait que… , Or…, Donc… ».

• Pour cela, il faut citer un théorème ou (ré)citer la propriété ou la règle utilisée.
• Par exemple : D’après le théorème de Thalès, on a… ou d’après la propriété qui dit que : « …je récite… », on peut affirmer que…
• Pour conclure, on dit « Donc… » ou « Par conséquent,… ».
• On utilise des mots de liaison « De plus,… », « Aussi,… », « Par ailleurs,… », « On sait aussi que… » etc…

4. Exercices résolus

Exercice résolu n°2.
Soit ${\mathcal C}$ le cercle de centre $O$ et de diamètre $AB=10~$cm.
Placer le point $M$ sur le cercle tel que $\widehat{BOM}=60^circ$.
Démontrer que le triangle $BOM$ est équilatéral.

Exercice résolu n°3.
${\mathcal C}$ le cercle de centre $O$ et de diamètre $AB=6~$cm.
Construire un triangle $ABC$, rectangle en $A$ et tel que $AC=8~$cm.
Placer le point $G$, mileu de $[BC]$.
1°) Démontrer que le triangle $BOG$ est rectangle.
2°) Démontrer que $AB=AG$.

Exercice résolu n°4.
Soit ${\mathcal C}$ le cercle de centre $O$ et de diamètre $AB=10~$cm.
Soit $M$ un point quelconque de cercle ${\mathcal C}$, différent de $A$ et $B$.
Démontrer que le triangle $AMB$ est rectangle en $M$.
Indication. On pourra construire le point $N$ symétrique de $M$ par rapport à $O$.

Exercice résolu n°5.
$ABCD$ est un carré et $AEB$ est un triangle équilatéral tracé à l’intérieur du carré $ABCD$.
$BCF$ est un triangle équilatéral tracé à l’extérieur du carré $ABCD$.
1°) Faire une figure avec $AB=6~$cm.
2°) Calculer la mesure de l’angle $\widehat{CDE}$
3°) Calculer la mesure de l’angle $\widehat{CDF}$
4°) En déduire que les trois points $D$, $E$ et $F$ sont alignés.