Distance entre deux points du plan. Longueur d’un segment. Alignement de trois points. Nature d’un triangle
Soient $(O ; I,J)$ un repère orthonormé du plan et $A$ et $B$ deux points de coordonnées $A(x_A ; y_A)$ et $B(x_B ; y_B)$. Dans cette page, nous donnons la formule qui permet de calculer la distance entre les deux points $A$ et $B$, qui est aussi la longueur du segment $[AB]$.
C’est une application directe du théorème de Pythagore. Nous devons calculer des distances donc, comme en primaire, nous devons avoir un repère orthogonal et la même unité sur les deux axes. Donc, nous devons travailler dans un repère orthonormé $(O; I,J)$ du plan.
1. Calcul de la longueur d’un segment
Théorème 3.
Le plan est muni d’un repère orthonormé $(O;I,J)$. Soient $A$ et $B$ deux points de coordonnées $A (x_A;y_A)$ et $B(x_B;y_B)$, alors la distance entre les deux points $A$ et $B$ est égale à la longueur du segment $[AB]$ et est donnée par la formule : $$\boxed{~~AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}~~}$$
Démonstration
Le repère $(O;I;J)$ étant orthonormé, les deux axes $(OI)$ et $(OJ)$ sont perpendiculaires.
Donc le triangle $ABK$ est rectangle en $K$. De plus $OI=OJ=1$, donc, nous avons la même unité sur les deux axes. Donc, d’après le théorème de Pythagore, on a : $$\begin{array}{rcl}
AB^2&=&AK^2+BK^2\\ AB^2 &=&(x_B-x_A)^2+(y_B-y_A)^2\\ AB&=&\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\\
\end{array}$$
D’où le résultat.
Exemple 1.
Dans un repère orthonormé $(O;I;J)$, on donne les points de coordonnées $A (–2 ; 3)$ et $B(4 ;1)$ et calculer la longueur du segment $[AB]$.
[Indication importante. J’écris exprès les points et leurs coordonnées les uns en dessous des autres pour calculer facilement les différences.]
$$\boxed{~~\begin{array}{r} A (–2~;~3)\\ B (~4~;~1)\\ \end{array}~~}$$
2. Nature d’un triangle
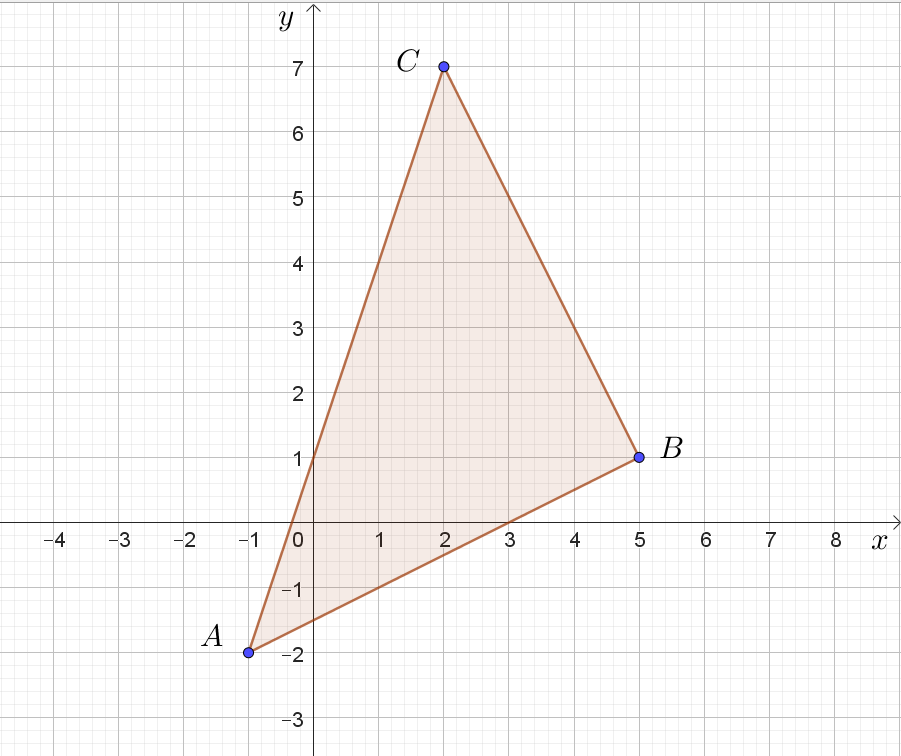
Exemple 2.
Dans un repère orthonormé $(O ; I ; J)$, placer les points $A(–1;–2)$ ; $B(5;1)$ et $C(2 ;7)$. Quelle est la nature du triangle $ABC$ ? Justifier votre réponse.
Corrigé.
Dans un repère orthonormé $(O;I,J)$, on place les points $A(–1;–2)$ ; $B(5;1)$ et $C(2 ;7)$.
1°) Conjecture : Par lecture graphique, à l’oeil nu, il semble que le triangle soit isocèle rectangle en $B$.
2°) Vérification par le calcul.
Le repère $(O;I;J)$ étant orthonormé, on calcule les longueurs :
$$\begin{array}{rcl} AB&=&\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\\ AB&=&\sqrt{(5+1)^2+(1+2)^2}\\ AB&=&\sqrt{6^2+3^2}\\ AB&=&\sqrt{36+9}\\ AB&=&\sqrt{45}\\ \end{array}$$
Donc : $\qquad\boxed{\;AB=\sqrt{45}\;}$
$$\begin{array}{rcl} BC&=&\sqrt{(x_B-x_C)^2+(y_B-y_C)^2}\\ BC&=&\sqrt{(2-5)^2+(7-1)^2}\\ BC&=&\sqrt{(-3)^2+6^2}\\ BC&=&\sqrt{9+36}\\ BC&=&\sqrt{45}\\ \end{array}$$
Donc : $\qquad\boxed{\;BC=\sqrt{45}\;}$
$$\begin{array}{rcl} AC&=&\sqrt{(x_C-x_A)^2+(y_C-y_A)^2}\\ AC&=&\sqrt{(2+1)^2+(7+2)^2}\\ AC&=&\sqrt{3^2+9^2}\\ AC&=&\sqrt{9+81}\\ AC&=&\sqrt{90}\\ \end{array}$$
Donc : $\qquad\boxed{\;AC=\sqrt{90}\;}$
Premières conclusions.
D’abord, on remarque que $AB = BC$ et $AB\not=AC$. Donc, le triangle $ABC$ est isocèle en $B$, mais il n’est pas équilatéral.
De plus, le côté le plus grand du triangle est $[AC]$. Cherchons si $ABC$ est rectangle ?
Je calcule séparément les carrés :
$$\left\lbrace\begin{array}{rcl} AC^2&=&\sqrt{90}^2=\boxed{\;90\;}\\ AB^2+BC^2&=&\sqrt{45}^2+\sqrt{45}^2=45+45=\boxed{\;90\;}\\
\end{array}\right.$$
On constate qu’on a bien l’égalité : $AC^2=AB^2+BC^2$.
Par conséquent, d’après la réciproque du théorème de Pythagore, le triangle $ABC$ est rectangle en $B$.
Conclusion. Le triangle $ABC$ est isocèle rectangle en $B$.