Décompositions additive et multiplicative d’une fraction

1. Différentes expressions d’une fraction

On découpe une pizza en 8 parts égales ou 8 morceaux égaux.

3 parts = $\dfrac{3}{8}$. On lit « trois-huitièmes ».

Mais on a aussi : $$\textbf{3 parts = 1 part + 1 part + 1 part.}$$
La même fraction peut donc s’écrire aussi. $$\boxed{\;\dfrac{3}{8}=\underbrace{\dfrac{1}{8}+\dfrac{1}{8}+\dfrac{1}{8}}_{\text{3 termes}}\;}$$ C’est la même part qui se répète 3 fois. On peut donc aussi écrire : $$\boxed{\;\dfrac{3}{8}=3\times\dfrac{1}{8}\;}$$

Plus généralement :

Propriété 1.
Si $a$ et $b$ sont deux nombres entiers, différents de $0$. Alors la fraction $\dfrac{a}{b}$ peut s’écrire de plusieurs manières : $$\begin{array}{c}
\boxed{~~\dfrac{a}{b}=\underbrace{\dfrac{1}{b}+\dfrac{1}{b}+\cdots+\dfrac{1}{b}}_\text{$a$ termes}~~}\\
\text{ou}\qquad\boxed{~~\dfrac{a}{b}=a\times\dfrac{1}{b}\\ ~~} \end{array}$$

Exemple 1.
Écrire chacune des fractions $\dfrac{2}{7}$, $\dfrac{3}{8}$ et $\dfrac{5}{3}$, de deux manières sous la forme d’une somme ou d’un produit.

Propriété 2.
pour tout nombre entier $b$, différent de $0$, on a : $$\dfrac{b}{b}=b\times\dfrac{1}{b}={\textbf 1}$$

2. Écrire avec une seule fraction $1+\dfrac{1}{3}$

Exemple 2.
Et si on prenait deux pizzas et on donne à Camille la première pizza et $\dfrac{1}{3}$ de la deuxième. Quelle « fraction » « F » de pizza a-t-elle obtenu ?

Ici, on a découpé la deuxième pizza en trois parts. Découpons aussi la première en trois parts. Camille obtient : La première pizza entière + Un tiers de la deuxième. Ce qui donne :
Comme 1 pizza = 1 = $3\times\dfrac{1}{3}$, la « fraction » « F » de pizza que Camille obtient est : $$1+\dfrac{1}{3}=3\times\dfrac{1}{3}+\dfrac{1}{3}=\dfrac{4}{3}$$
Ce qui donne finalement les 4 écritures de la même fraction $\dfrac{4}{3}$. $$\begin{array}{c}
\boxed{\;\dfrac{4}{3} = \dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3} \;}\\
\boxed{\; \dfrac{4}{3} = 4\times\dfrac{1}{3} \;}\\ \boxed{\; \dfrac{4}{3} = 1+\dfrac{1}{3} \;}\\
\end{array}$$

Exemples
Si on découpe une pizza en 5 parts égales, et qu’on prenne les 5 parts, on a pris 1 pizza entière. Donc : $$\boxed{\; 5\times\dfrac{1}{5}=1 \;}$$
D’une manière analogue : $$\boxed{\; 10\times\dfrac{1}{5}=2 \;}$$ et $$\boxed{\; 30\times\dfrac{1}{5}=6 \;}$$

2. Exercices résolus

Exemple 2.
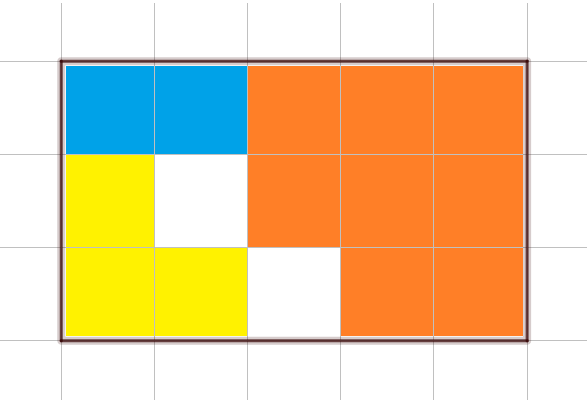
Construire un rectangle de longueur 5 carreaux et de largeur 3 carreaux. Écrire chacune des fractions $\dfrac{2}{15}$, $\dfrac{3}{15}$ et $\dfrac{8}{15}$, de deux manières sous la forme d’une somme ou d’un produit.

---

Exemple 3.
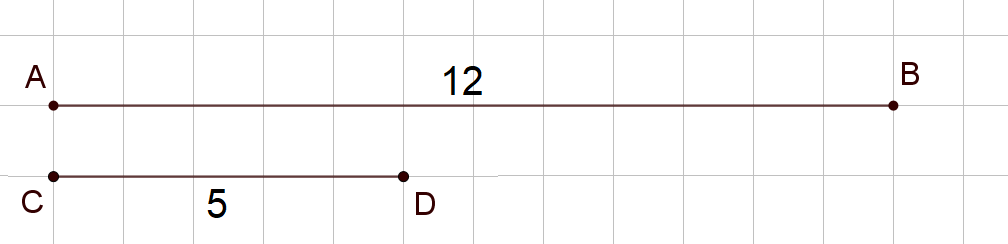
Construire un segment $[AB]$ de longueur $12$ cm.
1°a) Construire un segment $[CD]$ de longueur $5$ cm.
b) Quelle fraction du segment $[AB]$, représente le segment $[CD]$ ?
c) On peut écrire : $$CD = \dfrac{\cdots}{\cdots} \times AB$$
2°) Construire un segment $[EF]$ de longueur $8$ cm.
a) Quelle fraction du segment $[AB]$, représente le segment $[EF]$ ?
b) On peut écrire : $$EF = \dfrac{\cdots}{\cdots} \times AB$$