Pré-requis :
$\bullet $ Expérience aléatoire. Issues. Événements
1. Probabilité d’un événement
1.1. Probabilité théorique
Définitions 3.
Pour certaines expériences aléatoires, sous certaines conditions, on peut déterminer en pourcentage ou par un quotient « la chance » qu’un événement a pour se réaliser. Ce nombre s’appelle la « probabilité » ou « probabilité théorique » de l’événement.
Exemple 1.
Le lancer d’un dé à 6 faces parfaitement équilibré. On dit que le dé est non pipé ou non truqué. L’univers de l’expérience aléatoire est $\Omega=\{1 ; 2 ; 3 ;4 ;5 ;6\}$.
On peut supposer donc que les six faces ont exactement la même chance d’apparaître.
Par conséquent, la probabilité théorique de l’apparition de chaque face est de $\dfrac{1}{6}$.
Si on note $E_1$ = « obtenir la face 1″, on a $E_1=\{1\}$ et $P(E_1)=\dfrac{1}{6}$.
On note de même $E_k$ = »obtenir la face k« , $k=1;2;…;6$, alors $E_k=\{k\}$ et $P(E_k)=\dfrac{1}{6}$ Ce qui donne, pour tout $k=1;2;…6$ : $$P(E_k)=\dfrac{1}{6}\simeq 0,16666\ldots$$
On peut aussi écrire en langage symbolique : $$P(\omega)=\dfrac{1}{6} \simeq0,16666\ldots$$ pour tout $\omega\in\Omega$.
De même, si $A$ = »le résultat est pair » alors $A=\{2;4;6\}$ et $A$ a trois chances sur six d’être réalisé. Donc $P(A)=\dfrac{3}{6}=\dfrac{1}{2}$, qu’on peut écrire $P(A)=0,5$ ou encore $50\%$.
Remarque
La probabilité d’un événement est un nombre compris entre 0 et 1 qui s’écrit :
- sous la forme fractionnaire (numérateur inférieur au dénominateur) ;
- ou sous la forme d’un pourcentage (valeur arrondie en général) ;
- ou encore sous la forme d’un nombre décimal (valeur arrondie en général).
Exemple 2.
Une urne contient 10 boules de même dimension et indiscernables au toucher et numérotées : deux blanches $B_1$ et $B_2$ ; trois rouges, $R_1$, $R_2$ et $R_3$ et cinq boules vertes $V_1$, $V_2$,… $V_5$. On tire une boule de cette urne et on note sa couleur et son
numéro. On peut supposer donc que les dix boules ont exactement la même chance
d’être tirées. Par conséquent, la probabilité théorique du tirage de chaque boule est de $\dfrac{1}{10}$.
Si $R$ désigne l’événement « la boule tirée est rouge » alors $R=\{R_1,R_2,R_3\}$ et
Donc $P(R)=\dfrac{1}{10}$ qu’on peut aussi écrire $P(R)=0,3=\dfrac{30}{100}$, donc $P(R)=30\%$.
2. Probabilité et fréquence
Théorème 1. (Loi des grands nombres)
Si on répète une expérience aléatoire un très grand nombre de fois, les fréquences de
réalisation de n’importe quel événement se rapprochent et finissent par se stabiliser
autour de la probabilité théorique de l’événement.
Remarque
Si on lance un dé plusieurs fois, même s’il est « parfaitement équilibré », nous ne
sommes pas sûrs que chaque face aura « exactement » 1 chance sur 6 d’apparaître !!
C’est pourquoi, nous parlons de « probabilité théorique » car, dans la pratique, les
réalisations sont « aléatoires » donc imprévisibles. Mais le théorème nous affirme
que, si on recommence un grand nombre de fois, nous nous approchons de cette
probabilité théorique,…
Exemple 3.
Activité : Simulation de plusieurs lancers d’un dé parfaitement équilibré.
Nous avons vu que la probabilité théorique de chaque événement élémentaire pour le lancer d’un dé parfaitement équilibré, est : $$P(\omega)=\dfrac{1}{6}\simeq0,16666\ldots$$ pour tout $\omega\in\Omega$.
A l’aide d’un tableur, nous réalisons cette simulation en utilisant les fonctions ALEA()
ENT(-) et NB.SI(- ;-). Nous avons obtenu les résultats suivants avec
la simulation de 100 lancers aléatoires :
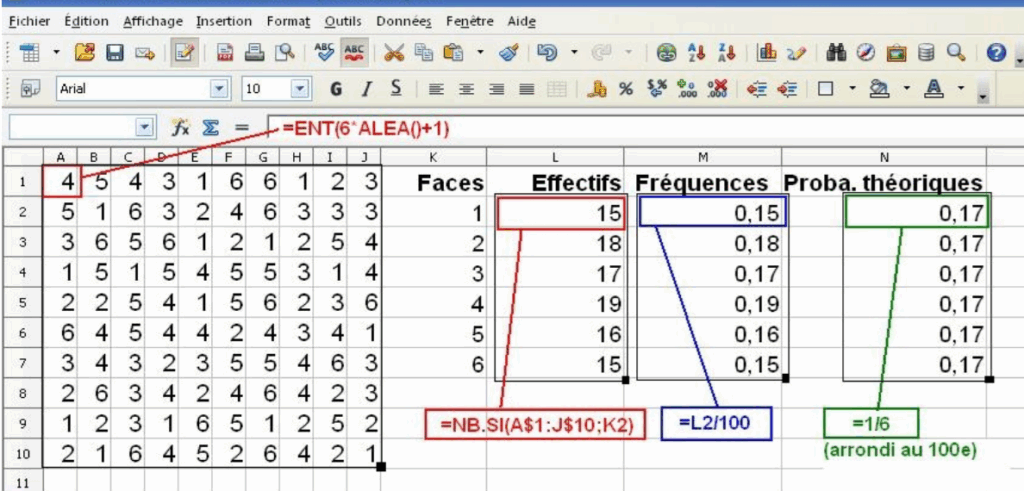
Au lieu d’utiliser une fonction composée ENT(6*ALEA()+1), on peut aussi utiliser la fonction ALEA.ENTRE.BORNES(1,6) qui renvoie un nombre entier aléatoire entre les nombres que vous spécifiez. Un nouveau nombre entier aléatoire est renvoyé chaque fois que la feuille de calcul est calculée (F9).
Évidemment, nous pouvons recommencer la même procédure avec 1000 valeurs (on
arrondit au 1000ème), puis 10000, puis 100 000 valeurs, nous obtenons des
fréquences très proches de 0,1666…
3. Calculs et loi de probabilités
Définition 4.
Pour définir les probabilités des événements associés à une expérience aléatoire, on
définit les probabilités de tous les événements élémentaires. On dit qu’on a donné la
loi de probabilité de cette expérience.
Exemple 4.
La loi de probabilité du lancer d’un dé parfaitement équilibré est donnée par : pour tout $\omega\in\Omega$ $P(\omega)=\dfrac{1}{6}\simeq0,16666\ldots$.
6 . On peut aussi écrire la loi de probabilité dans un tableau :
$$\begin{array}{|c|c|c|c|c|c|c|c|}\hline \text{Issues }\omega& 1& 2& 3& 4& 5& 6& \text{Total}\\ \hline
P({ω}) & \dfrac{1}{6}& \dfrac{1}{6}& \dfrac{1}{6}& \dfrac{1}{6}& \dfrac{1}{6}& \dfrac{1}{6}& 1\\ \hline
\end{array}$$
4. Exercices résolus
Exercice résolu 1.
Dans un tableur, refaire la simulation de 1000 lancers d’un dé parfaitement équilibré.
Exercice résolu 2.
Un dé est truqué de telle façon que la probabilité de chaque face est proportionnelle
au numéro de la face. On lance le dé truqué et on note le numéro de la face supérieure. 1°) Donner la loi de probabilité de cette expérience aléatoire.
2°) Calculer la probabilité de l’événement $A$ = « le résultat est pair »

