Soient $(O ; I,J)$ un repère quelconque du plan et $A$ et $B$ deux points de coordonnées $A(x_A ; y_A)$ et $B(x_B ; y_B)$. Dans cette page, nous donnons la formule qui permet de calculer les coordonnées du milieu $M$ du segment $[AB]$.

C’est une application directe du théorème de la droite des milieux.

  1. Repérage d’un point dans le plan. Coordonnées cartésiennes
  2. Coordonnées du milieu d’un segment dans le plan
  3. Distance entre deux points du plan. Longueur d’un segment. Alignement de trois points
  4. Vecteurs et coordonnées dans le plan. Base de l’ensemble des vecteurs du plan
  5. Distance entre deux points du plan. Nature d’un triangle

1. Coordonnées du milieu d’un segment

Théorème 1.
Dans un repère quelconque $(O ;I,J)$, si $A$ et $B$ sont deux points de coordonnées $A(x_A ; y_A)$ et $B(x_B ; y_B)$, alors le milieu $M$ du segment $[AB]$ a pour coordonnées :
$$\boxed{~~\begin{array}{l} \phantom{\text{et}}~~x_M = \dfrac{x_A+x_B}{2}\\
\text{et}~~y_M = \dfrac{y_A+y_B}{2}\\ \end{array}~~}$$

2. Exercices résolus

Exemple 1.
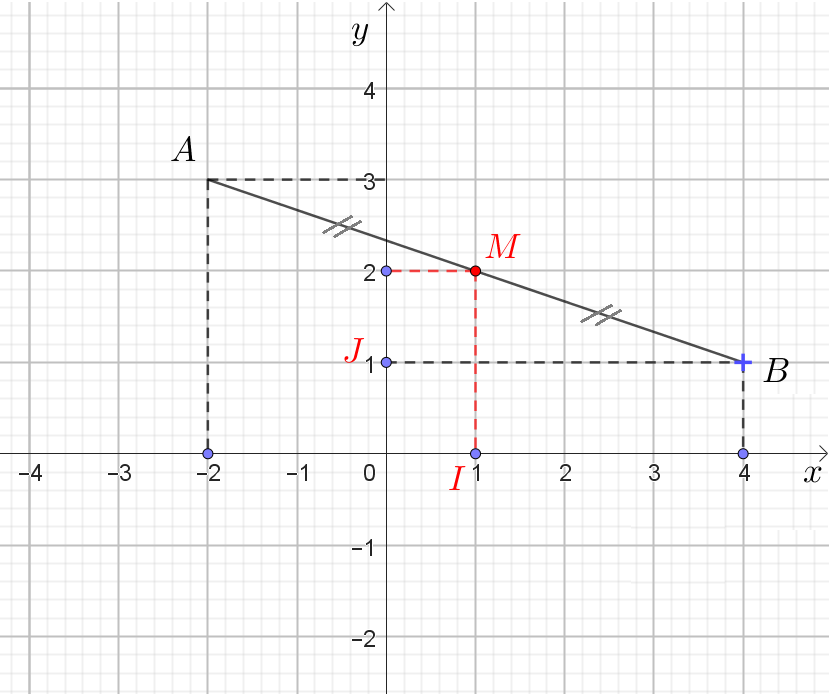
Dans un repère orthonormé $(O;I;J)$, placer les points $A(–2 ; 3)$ et $B (4 ;1)$.
1°) Déterminer graphiquement les coordonnées du milieu $M$ du segment $[AB]$.
2°) Calculer les coordonnées du milieu $M$ du segment $[AB]$.

Corrigé.
1°) Dans un repère orthonormé $(O;I;J)$, placer les points $A(–2 ; 3)$ et $B (4 ;1)$.
Par lecture graphique, il semble que le milieu $M$ du segment $[AB]$ a pour coordonnées : $$\boxed{~~M(1;2)~~}$$

2°) D’après le cours, on sait que les coordonnées du milieu $M$ du segment $[AB]$ sont données par la formule :
$$\left\lbrace \begin{array}{l}
x_M = \dfrac{x_A+x_B}{2}=\dfrac{-2+4}{2}=\dfrac{2}{2}=\boxed{1}\\
y_M = \dfrac{y_A+y_B}{2}=\dfrac{1+3}{2}=\dfrac{4}{2}=\boxed{2}\\
\end{array} \right.$$
Conclusion. les coordonnées du milieu $M$ du segment $[AB]$ sont $$\boxed{~~M(1;2)~~}$$ CQFD.$\blacktriangle$

Exemple 2.
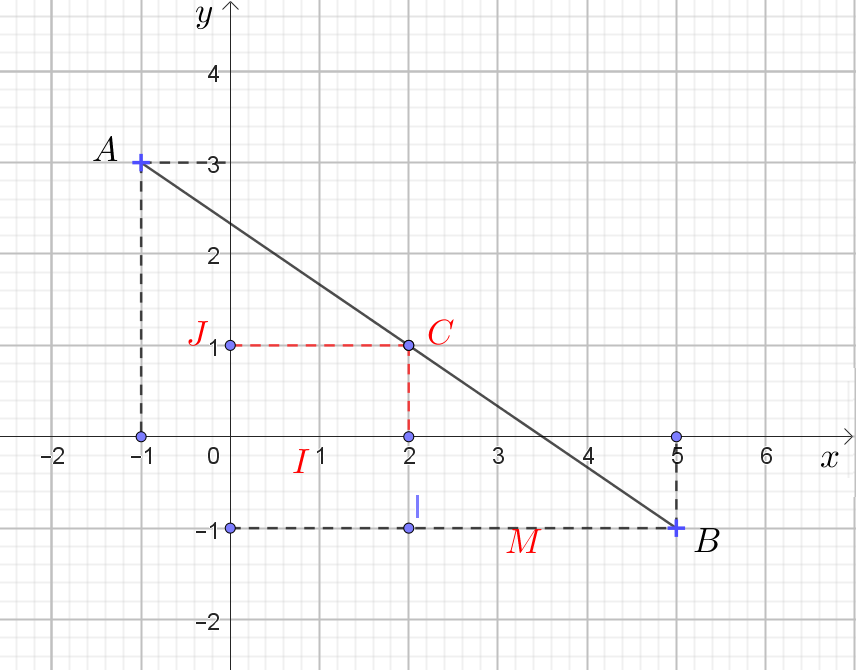
Dans un repère orthonormé $(O;I,J)$, on considère les deux points $A(-1 ; 3)$ et $B$ et $C(2;1)$
1°) Placer les deux points $A$ et $C$ dans le repère orthonormé $(O;I,J)$.
2°) Déterminer graphiquement les coordonnées du point $B$ sachant que $C(2;1)$ est le milieu du segment $[AB]$.
3°) Calculer les coordonnées du point $B$.

Corrigé.
1°) Placer les deux points $A$ et $C$ dans le repère orthonormé $(O;I,J)$.
2°) Le point $C$ est le milieu du segment $[AB]$. Donc, $B$ est le symétrique de $A$ par rapport à $C$. Et, par lecture graphique, il semble que le point $B$ ait pour coordonnées : $$\boxed{~~B(5;-1)~~}$$

Coordonnées du milieu d'un segment dans le plan

3°) D’après le cours, on sait que les coordonnées du milieu $C$ du segment $[AB]$ sont données par la formule suivante. On résout alors un système de deux équations, chacune à une inconnue. [Nous utilisons l’égalité des produits en croix pour l’égalité des fractions] :
$$ \begin{array}{rcl}
\left\lbrace \begin{array}{l} x_C = \dfrac{x_A+x_B}{2}\\
y_C = \dfrac{y_A+y_B}{2}\\ \end{array} \right.
&\Leftrightarrow& \left\lbrace \begin{array}{l}
2=\dfrac{-1+x_B}{2}\\ 1 = \dfrac{3+y_B}{2}\\ \end{array} \right. \\ &\Leftrightarrow& \left\lbrace \begin{array}{l}
-1+x_B=2\times2\\ 3+y_B=1\times 2\\ \end{array} \right. \\
&\Leftrightarrow& \left\lbrace \begin{array}{l}
x_B=4+1\\ y_B=2-3\\ \end{array} \right. \\
&\Leftrightarrow& \left\lbrace \begin{array}{l}
x_B=5\\ y_B=-1\\ \end{array} \right. \\
\end{array} $$
Conclusion. les coordonnées du point $B$ sachant que $C(2;1)$ est le milieu du segment $[AB]$ sont $$\boxed{~~B(5;-1)~~}$$ CQFD.$\blacktriangle$