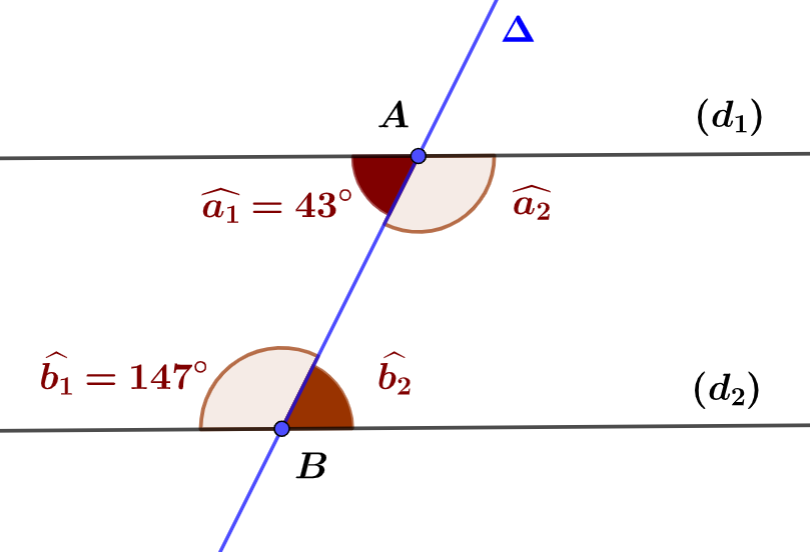
Nous avons vu (angles alternes-internes) que si deux droites $(d_1)$ et $(d_2)$ sont parallèles et coupées par une droite sécante $\Delta$ en deux points $A$ et $B$ respectivement, alors les angles alternes-internes sont de même mesure.

Dans cette page, nous étudions la propriété réciproque et sa contraposée. A savoir,

Si deux droites $(d_1)$ et $(d_2)$ sont coupées par une droite sécante $\Delta$ en formant deux angles alternes-internes de même mesure, peut-on affirmer ou non que les droites $(d_1)$ et $(d_2)$ sont parallèles ? La réponse est OUI.

D’autre part, si deux droites $(d_1)$ et $(d_2)$ sont coupées par une droite sécante $\Delta$ en formant deux angles alternes-internes de mesures différentes, peut-on affirmer ou non que les droites $(d_1)$ et $(d_2)$ ne sont pas parallèles ? La réponse est OUI.

1. Comment justifier que deux droites sont parallèles ?

Figure 1.

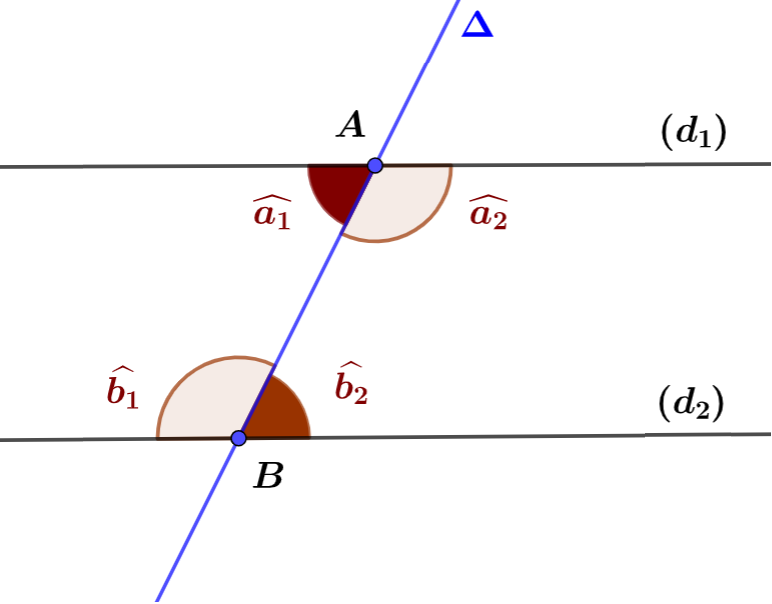
Propriété n°1. (Propriété réciproque).
Si deux droites $(d_1)$ et $(d_2)$ sont coupées par une droite sécante $\Delta$ en deux points $A$ et $B$ respectivement en formant deux angles alternes-internes de même mesure, Alors les droites $(d_1)$ et $(d_2)$ sont parallèles.
Autrement dit :
$$\boxed{~\text{Si}~\widehat{a_1}=\widehat{b_2}\quad\text{ou bien }~\text{si}~~\widehat{a_2}=\widehat{b_1},\quad\text{Alors}~d_1 // d_2~}$$

2. Comment justifier que deux droites ne sont pas parallèles ?

Propriété n°2. (Propriété contraposée).
Si deux droites $(d_1)$ et $(d_2)$ sont coupées par une droite sécante $\Delta$ en deux points $A$ et $B$ respectivement en formant deux angles alternes-internes de mesures différentes, Alors les droites $(d_1)$ et $(d_2)$ ne sont pas parallèles.
Autrement dit :
$$\boxed{~\text{Si}~\widehat{a_1}\not=\widehat{b_2}\quad\text{ou bien }~\text{si}~~\widehat{a_2}\not=\widehat{b_1},\quad\text{Alors}~d_1 //\!\!\!\!\!\diagdown~d_2~}$$

3. Exercices résolus

Exercice résolu n° 1.
Avec les données indiquées dans la figure 2 ci-dessous, peut-on justifier que les droites $(d_1)$ et $(d_2)$ sont parallèles ou non ? Justifiez votre réponse.

Figure 2.

Je remarque d’abord que les angles dont on connaît les mesures dans cette figure ne sont pas alternes-internes.
Je commence par calculer la mesure de $\widehat{a_2}$ ou $\widehat{b_2}$.

a) Calcul de $\widehat{b_2}$.
On sait que $\widehat{b_1}=141°$ et les deux angles $\widehat{b_1}$ et $\widehat{b_2}$ sont adjacents et forment un angle plat. Ils sont donc supplémentaires.
Donc : $$\widehat{b_1}+\widehat{b_2}=180°$$ Donc : $$141°+\widehat{b_2}=180°$$ Ce qui donne : $$\widehat{b_2}=180°-141°$$ D’où : $$\boxed{~\widehat{b_2}=39°~}$$

b) Les droites $(d_1)$ et $(d_2)$ sont-elles parallèles ?
On sait que $\widehat{a_1}=39°$ et $\widehat{b_2}=39°$ Donc :
$$\boxed{~\widehat{a_1}=\widehat{b_2}=39°~}$$
D’autre part, les deux droites $(d_1)$ et $(d_2)$ sont coupées par une droite sécante $\Delta$ en formant deux angles alternes-internes de même mesure, Donc, les droites $(d_1)$ et $(d_2)$ sont parallèles.
Conclusion. Les droites $(d_1)$ et $(d_2)$ sont parallèles.
CQFD. $\blacktriangle$

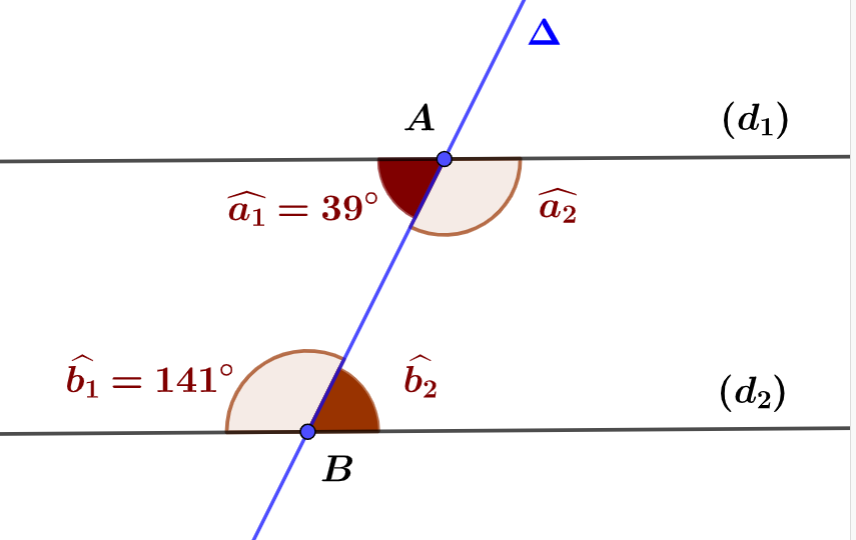
Exercice résolu n° 2.
Avec les données indiquées dans la figure 3 ci-dessous, peut-on justifier que les droites $(d_1)$ et $(d_2)$ sont parallèles ou non ? Justifiez votre réponse.

Figure 3.

Je remarque d’abord que les angles dont on connaît les mesures dans cette figure ne sont pas alternes-internes.
Je commence par calculer la mesure de $\widehat{a_2}$ ou $\widehat{b_2}$.

a) Calcul de $\widehat{b_2}$.
On sait que $\widehat{b_1}=147°$ et les deux angles $\widehat{b_1}$ et $\widehat{b_2}$ sont adjacents et forment un angle plat. Ils sont donc supplémentaires.
Donc : $$\widehat{b_1}+\widehat{b_2}=180°$$ Donc : $$147°+\widehat{b_2}=180°$$ Ce qui donne : $$\widehat{b_2}=180°-147°$$ D’où : $$\boxed{~\widehat{b_2}=33°~}$$

b) Les droites $(d_1)$ et $(d_2)$ sont-elles parallèles ?
On sait que $\widehat{a_1}=43°$ et $\widehat{b_2}=33°$. Donc :
$$\boxed{~\widehat{a_1}\not=\widehat{b_2}~}$$
D’autre part, les deux droites $(d_1)$ et $(d_2)$ sont coupées par une droite sécante $\Delta$ en formant deux angles alternes-internes de mesures différentes, Donc, les droites $(d_1)$ et $(d_2)$ ne sont pas parallèles.
Conclusion. Les droites $(d_1)$ et $(d_2)$ ne sont pas parallèles.
CQFD. $\blacktriangle$