1. Symétrique d’un polygone par une symétrie axiale

Nous avons déjà vu comment construire le symétrique d’un point par rapport à une droite, à l’équerre, puis à la règle et au compas.
Deux figures symétriques par rapport à un axe $\Delta$ sont superposables.

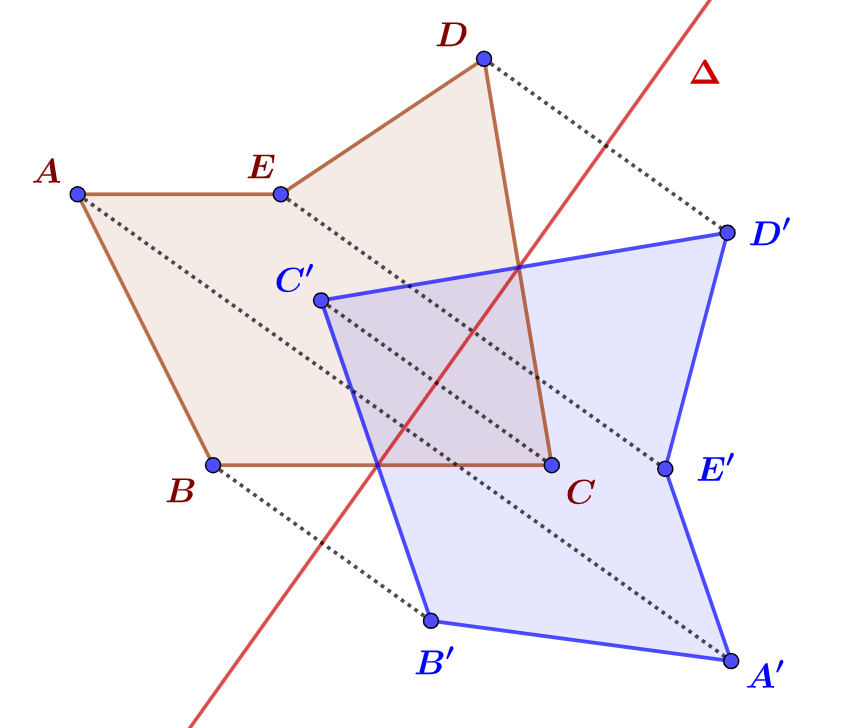
Propriétés n°1. (Figure 1.)
$(P_4)$. Le symétrique d’un polygone $ABCDE$ par rapport à une droite est un polygone $A’B’C’D’E’$ superposable.

Pour construire le symétrique d’un d’un polygone $ABCDE$, il suffit de construire le symétrique de chacun des sommets $A$, $B$, $C$, $D$ et $E$ du polygone, puis relier pour obtenir un polygone $A’B’C’D’E’$ superposable.

Figure 1. $A’B’C’D’E’$, symétrique d’un d’un polygone $ABCDE$
Haut de page

2. Symétrique d’un cercle par une symétrie axiale

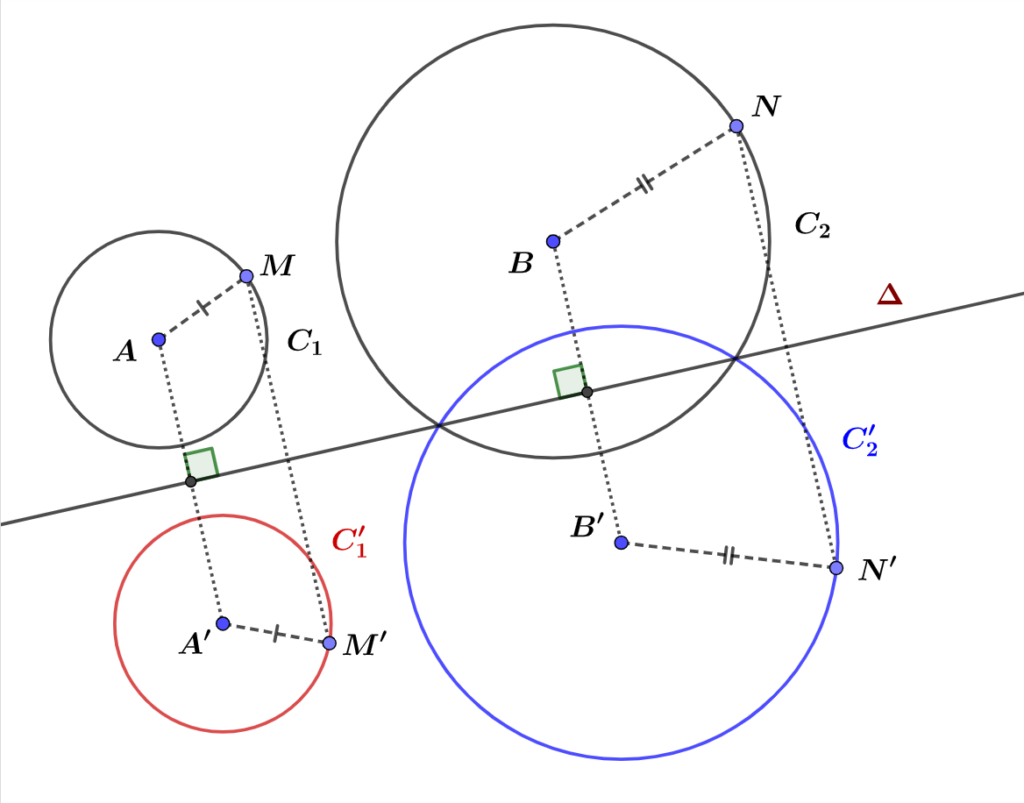
Propriétés n°2. (Figure 2.)
$(P_6)$. Le symétrique d’un cercle de centre $A$ et de rayon $r$ par rapport à une droite est un cercle de centre $A’$, symétrique de $A$ et de même rayon $r$.

Pour construire le symétrique d’un cercle, on construit les symétriques du centre et d’un point du cercle. Puis on reconstruit un deuxième cercle de même rayon.

Figure 2. Le symétrique d’un cercle est un cercle de même rayon $r$.
Haut de page

3. Symétrique d’un angle par une symétrie axiale

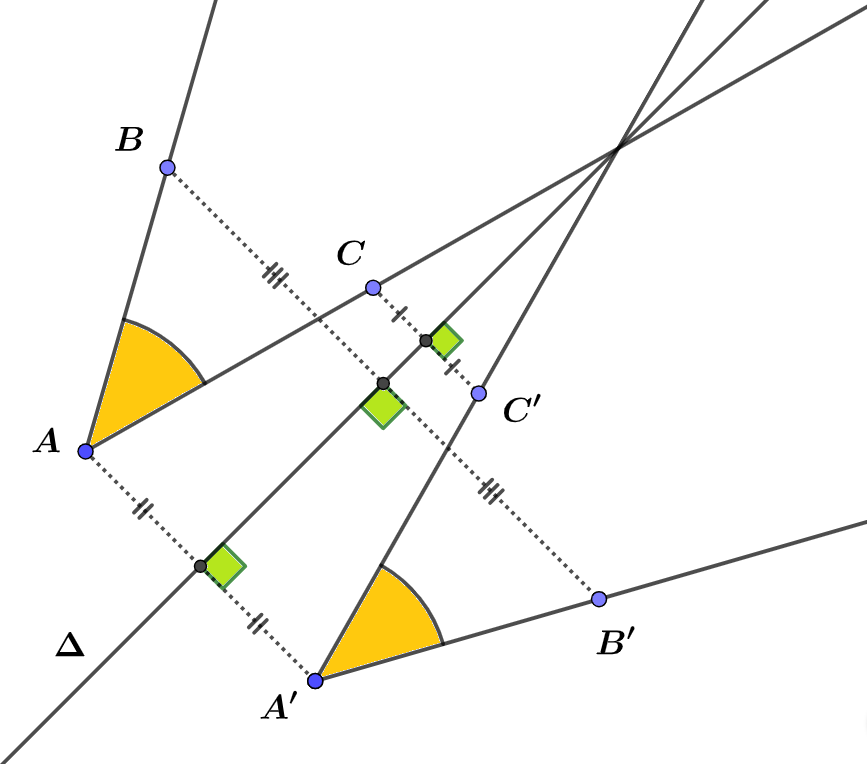
Propriétés n°3.
$(P_7)$. Le symétrique d’un angle $\widehat{xAy}$ par rapport à une droite est un angle $\widehat{x’A’y’}$ de même mesure. $$\boxed{~\widehat{x’A’y’}=\widehat{xAy}~}~~\text{et}~~\boxed{~\widehat{B’A’C’}=\widehat{BAC}~}$$

Pour construire le symétrique d’un angle, on construit les symétriques du sommet de l’angle et d’un point sur chaque côté de l’angle… Puis on reconstruit un deuxième angle de même mesure avec ces points.

Figure 3. $\widehat{x’A’y’}$ est le symétrique de $\widehat{xAy}$ par rapport à la droite $\Delta$
Haut de page

4. Exercices résolus

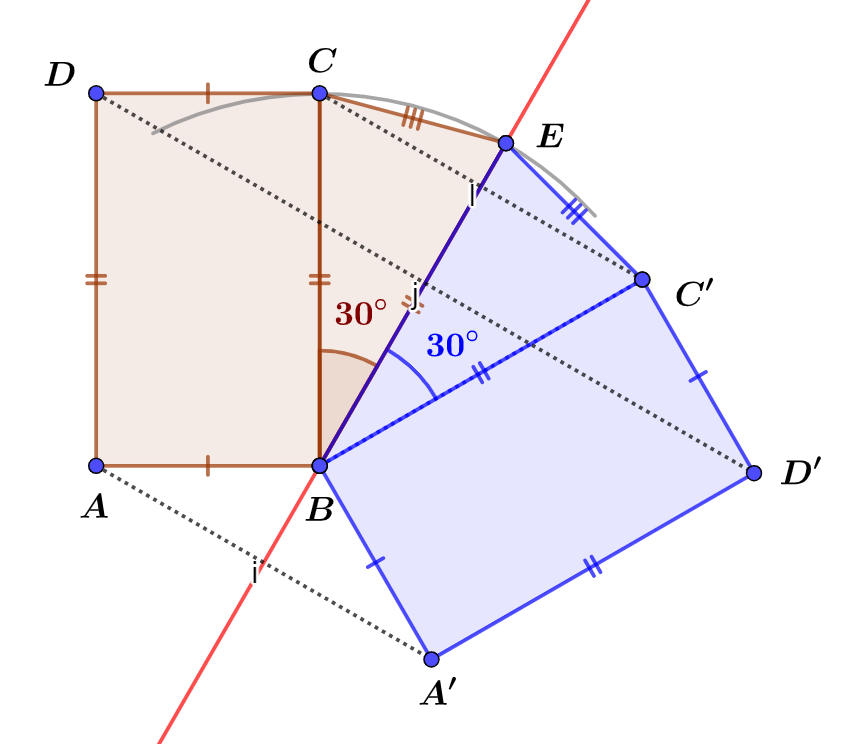
Exercice résolu n°1.
Construire un carré $ABCD$ de largeur $AB=$3cm et de longueur $BC=5$cm. Placer un pont $E$ à l’extérieur du rectangle $ABCD$ avec $BCE$ soit un triangle isocèle en $B$ et $\widehat{CBE}=30°$.
1°) Construire le symétrique du polygone $ABECD$ par rapport à l’axe $(BE)$.
2°) Quelle est la nature du triangle $BCC’$ ? Justifier votre réponse.

1°) $A’BEC’D$ est le symétrique de $ABECD$ par rapport à l’axe $(\Delta)$

2°) Quelle est la nature du triangle $BCC’$ ? Justifier votre réponse.
$BC’E$ est le symétrique du triangle $BCE$ par rapport à l’axe $(BE)$. Donc, en particulier, $$BC’=BC~~\text{et}~~\widehat{C’BE}=\widehat{CBE}=30°$$ Ce qui montre que le triangle $BCC’$ est isocèle en $B$ et $\widehat{CBC’}=2\times30=60°$. Les deux angles à la base sont de même mesure.
Donc : $\widehat{BCC’}=\widehat{BC’C}=(180-60)\div2=60°$
Par conséquent, le triangle $BCC’$ a trois angles de même mesure. Donc, $BCC’$ est un triangle équilatéral.
CQFD.$\blacktriangle$

Haut de page