1. Qu’est-ce qu’une fraction ?
Définition 1. Larousse.fr
Fractionner, verbe transitif : Diviser une totalité en parties, on dit « en fractions ».
Partager quelque chose en plusieurs morceaux ou en plusieurs groupes.
Définition 2.
Une fraction est une partie d’une unité divisée en parts égales.
Exemple 1. Illustration.
On découpe une pizza en 8 parts égales ou en 8 morceaux égaux.
Il y a une seule pizza $\rightarrow$ donc l’unité choisie est = 1 pizza.
On a découpé la pizza en 8 parts égales. 1 pizza = les 8 parts égales = $8\times\dfrac{1}{8}$.
1 part bleue = la fraction $\dfrac{1}{8}$. On lit « 1 sur 8 » ou « un-huitième ».
De même :
3 parts orange = $\dfrac{3}{8}$. On lit « 3 sur 8 » ou « trois-huitièmes ».
2. Écriture et lecture d’une fraction
Définition 3.
Dans la fraction $\dfrac{3}{8}$, le nombre en haut $3$ est le numérateur (N comme le Nord, en haut ) et la nombre en bas $8$ est le dénominateur. $$\dfrac{\boxed{3}}{\boxed{8}}=\dfrac{\boxed{\phantom{1}\cdot}}{\boxed{\phantom{1}\cdot}}~~\begin{array}{l} \leftarrow~\textit{numérateur} \\ \leftarrow~\textit{dénominateur} \\ \end{array}$$
D’une manière analogue :
2 parts = $\dfrac{2}{8}$ On lit « 2 sur 8 » ou « deux-huitièmes ».
4 parts = $\dfrac{4}{8}$ On lit « 2 sur 8 » ou « quatre-huitièmes ».
5 parts = $\dfrac{5}{8}$ On lit « 5 sur 8 » ou « cinq-huitièmes ».
Et ainsi de suite$\ldots$
8 parts = $\dfrac{8}{8}=1$ pizza entière. On lit « 8 sur 8 » ou « huit-huitièmes ».
Cas particuliers
$\dfrac{1}{2}$ On lit « 1 sur 2 » ou « un demi ».
$\dfrac{1}{3}$ On lit « 1 sur 3 » ou « un tiers».
$\dfrac{1}{4}$ On lit « 1 sur 4 » ou « un quart ».
Pour les autres fractions, on lit le numérateur et on ajoute « ième » au dénominateur.
$\dfrac{5}{12}$ On lit « 5 sur 12 » ou « cinq-douzièmes ».
3. Différentes expressions d’une fraction
3 parts = $\dfrac{3}{8}$ On lit « trois-huitièmes ».
Mais on a aussi : 3 parts = 1 part + 1 part + 1 part.
La même fraction peut donc s’écrire aussi. $$\dfrac{3}{8}=\underbrace{\dfrac{1}{8}+\dfrac{1}{8}+\dfrac{1}{8}}_{\text{3 termes}}$$ C’est la même part qui se répète 3 fois. On peut donc aussi écrire :
$$\dfrac{3}{8}=3\times\dfrac{1}{8}$$
Plus généralement :
Propriété 1.
Si $a$ et $b$ sont deux nombres entiers. Alors la fraction $\dfrac{a}{b}$ peut s’écrire des deux manières : $$\begin{array}{c}
\boxed{~~\dfrac{a}{b}=\underbrace{\dfrac{1}{b}+\dfrac{1}{b}+\cdots+\dfrac{1}{b}}_\text{$a$ termes}~~}\\
\text{ou}\qquad\boxed{~~\dfrac{a}{b}=a\times\dfrac{1}{b}\\ ~~} \end{array}$$
4. Autre manière d’écrire une fraction
Dans cette image, nous avons 2 pizzas et six huitièmes de pizza. Chaque pizza est partagée en 8, donc : $$1~\text{pizza} = \dfrac{8}{8}$$ On peut donc écrire $$2+\dfrac{5}{8}=\dfrac{8}{8}+\dfrac{8}{8}+\dfrac{5}{8}$$ Ce qui donne : $$2+\dfrac{5}{8}=\dfrac{21}{8}$$ $2$ étant la partie entière et $\dfrac{5}{8}$ la partie fractionnaire (moins qu’une pizza).
Nous obtenons une troisième écriture de la fraction $\dfrac{21}{8}$ : $$\color{brown}{\boxed{\begin{array}{rcl}
\dfrac{21}{8}&=&\underbrace{\dfrac{1}{8}+\dfrac{1}{8}+\cdots+\dfrac{1}{8}}_\text{$21$ termes}\\
&=&21\times\dfrac{1}{8}\\ &=& 2+\dfrac{5}{8}\\ \end{array}}}$$
Remarques
1°) La dernière écriture « $2+\dfrac{5}{8}$ » s’écrit aussi : « $2\dfrac{5}{8}$ ».
2°) Lorsque le numérateur est plus grand que le dénominateur, $\dfrac{a}{b}$ est dite une « fraction impropre ». On a besoin d’une ou plusieurs unité en plus d’une fraction de l’unité (fraction inférieure à 1).
5. Exercices résolus
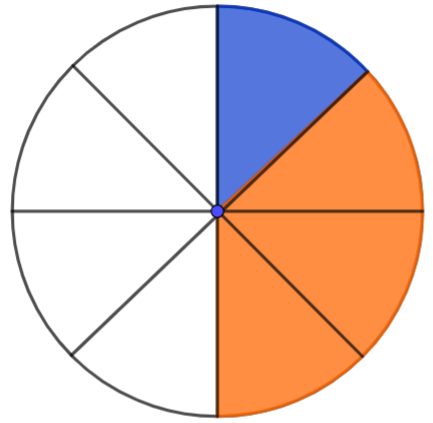
Exemple 2.
Dans la figure ci-dessus, déterminer la fraction de chaque couleur du disque. (Imaginez que c’est un gâteau ou une pizza.)
Exemple 3.
Construire un segment $[AB]$ de longueur $12$ cm.
1°a) Construire un segment $[CD]$ de longueur $5$ cm.
b) Quelle fraction du segment $[AB]$, représente le segment $[CD]$ ?
c) Compléter : $$CD = \dfrac{\cdots}{\cdots} \times AB$$
2°) Construire un segment $[EF]$ de longueur $8$ cm.
a) Quelle fraction du segment $[AB]$, représente le segment $[EF]$ ?
b) Compléter : $$EF = \dfrac{\cdots}{\cdots} \times AB$$
1°) Construction d’un segment $[AB]$ de longueur $12$ cm. Le segment $[CD]$ est de longueur $5$ cm. Donc :
a) Le segment $[CD]$ représente les cinq-douzièmes du segment $[AB]$.
b) On peut donc écrire : $$CD = \dfrac{5}{12} \times AB$$
2°) D’une manière analogue, le segment $[EF]$ est de longueur $8$ cm. Donc :
a) Le segment $[EF]$ représente les huit-douzièmes du segment $[AB]$.
b) On peut donc écrire : $$EF = \dfrac{8}{12} \times AB$$
CQFD.$\blacktriangle$
Exemple 4.
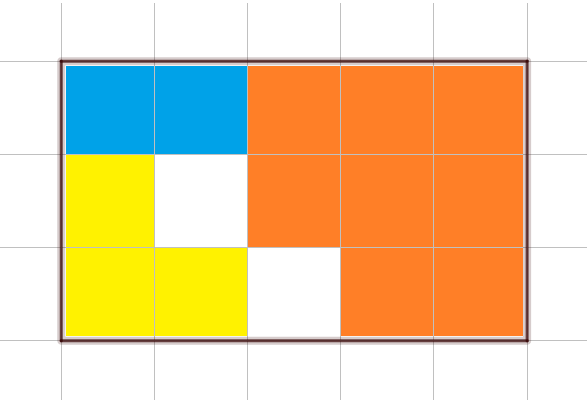
Construire un rectangle de longueur 5 carreaux et de largeur 3 carreaux.
1°) Colorier en bleu les $\dfrac{2}{15}$ème du rectangle.
2°) Colorier en jaune les $\dfrac{3}{15}$ème du rectangle.
3°) Et colorier en orange les $\dfrac{8}{15}$ème du rectangle.
4°) Quelle est la fraction qui reste en blanc ?
Construction du rectangle. Ici, le rectangle est partagé en $3\times5=15$ grands carreaux, donc en 15 parts égales. Chaque carreau représente donc « un-quinzième » du rectangle, qu’on écrit : $\dfrac{1}{15}$.
Pour colorier une fraction du rectangle, il suffit de compter les carreaux :
1°) La Zone bleue = 2 carreaux = « deux-quinzièmes » =$\dfrac{2}{15}$ème du rectangle.
2°) La Zone jaune = 3 carreaux = « trois-quinzièmes » =$\dfrac{3}{15}$ème du rectangle.
3°) La Zone orange = 8 carreaux = « huit-quinzièmes » =$\dfrac{8}{15}$ème du rectangle.
4°) Il reste deux carreaux en blanc. Ils représentent les $\dfrac{2}{15}$ème du rectangle.
CQFD.$\blacktriangle$