- La symétrie axiale
- Axe de symétrie
- Symétrique d’un point par rapport à une droite $(d)$
- Construction du symétrique d’un point à la règle et l’équerre
- Construction du symétrique d’un point à la règle et au compas.
- Construction du symétrique d’un segment
- Construction du symétrique d’une figure géométrique
- Exercices résolus
1. La symétrie axiale
1.1. Figures symétriques par rapport à une droite
Définition 1.
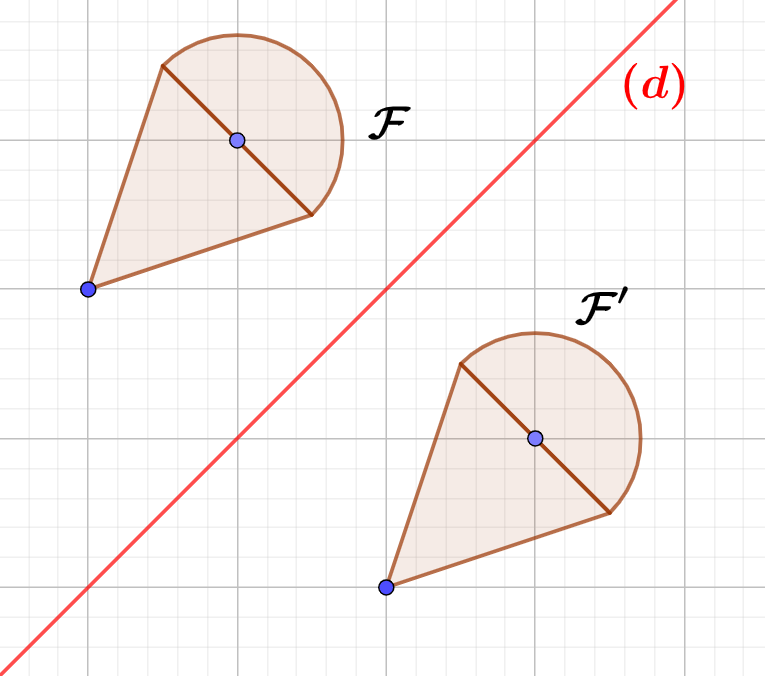
Deux figures sont symétriques par rapports à une droite $(d)$ lorsqu’elles se superposent exactement par pliage autour de la droite $(d)$.
1.2. Axe de symétrie
Définition 2.
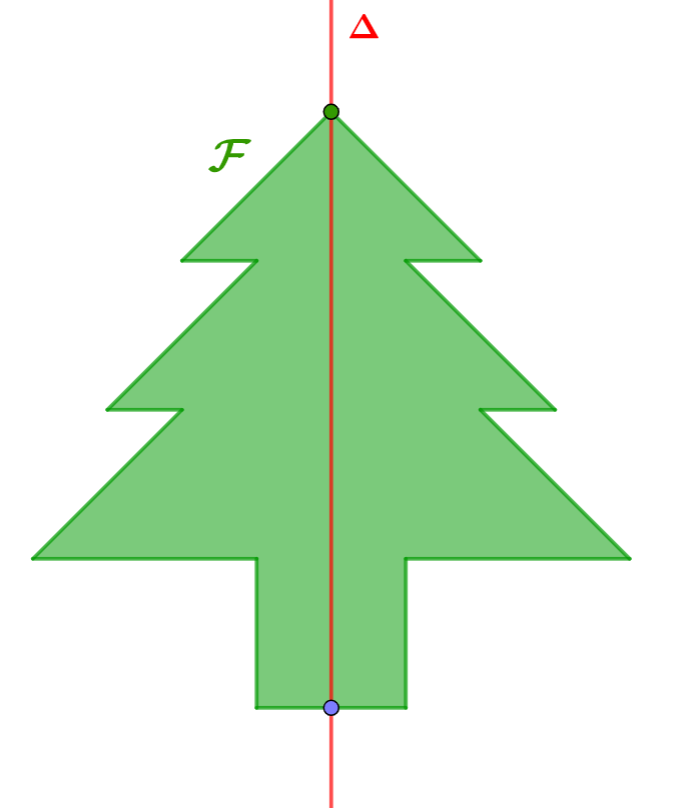
Un figure $\mathcal F$ admet la droite $\Delta$ (Lire « Delta ») comme axe de symétrie lorsque le symétrique de la figure $\mathcal F$ par rapport à la droite $\Delta$ est égal à la figure $\mathcal F$ elle-même.
On dit que la droite $\Delta$ est un axe de symétrie de la figure $\mathcal F$.
2. Construction du symétrique d’une figure
2.1. Symétrique d’un point par rapport à une droite $(d)$
Soit $(d)$ une droite et $M$ un point quelconque du plan. On distingue deux cas possibles :
- 1er cas : $M$ appartient à la droite $(d)$, on écrit : $M\in(d)$.
- 2ème cas : $M$ n’appartient pas à la droite $(d)$, on écrit : $M\not\in(d)$.
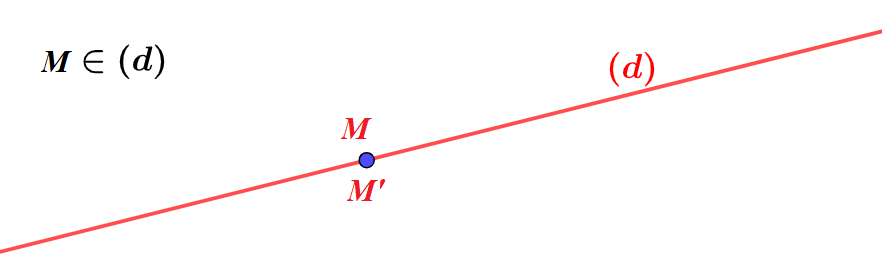
Définition 3. Premier cas $A\in(d)$.
Soit $M$ un point appartenant à la droite $(d)$, alors le symétrique de $M$ par rapport à la droite $(d)$ est égal au point $M$ lui-même.
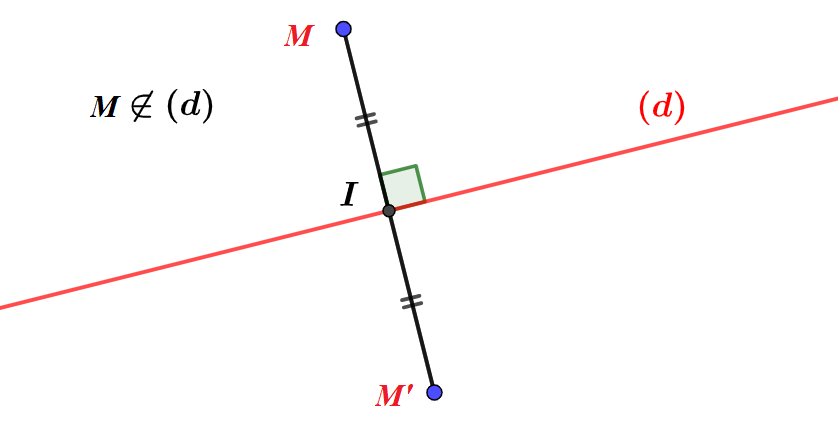
Définition 4. Deuxième cas $A\not\in(d)$.
Soit $M$ un point n’appartenant à la droite $(d)$, alors le symétrique de $M$ par rapport à la droite $(d)$ est le point $M’$ tel que $(d)$ soit la médiatrice du segment $[MM’]$.
2.2. Construction à la règle et l’équerre
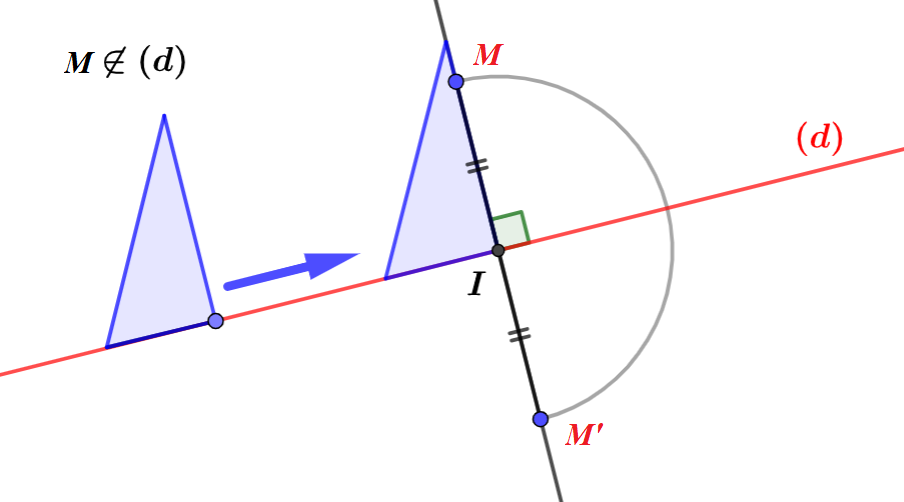
- Construire la droite $(d)$ et placer un point $M$ n’appartenant à la droite $(d)$.
- Placer l’équerre sur la droite $(d)$. Puis, faire glisser l’équerre sur la droite $(d)$ jusqu’au point $M$.
- Tracer la perpendiculaire à $(d)$ passant par $M$.
- Elle coupe la droite $(d)$ en un point $I$.
- Finalement, à partir de $I$, placer un point $M’$ de l’autre côté de $I$ tel que $MI=IM’$.
Ou bien, au compas construire un demi-cercle qui passe par $M$. Ce demi-cercle coupe $(MI)$ en $M’$. - $M’$ est le symétrique de $M$ par rapport à la droite $(d)$. CQFD.$\blacktriangle$
2.3. Construction à la règle et au compas
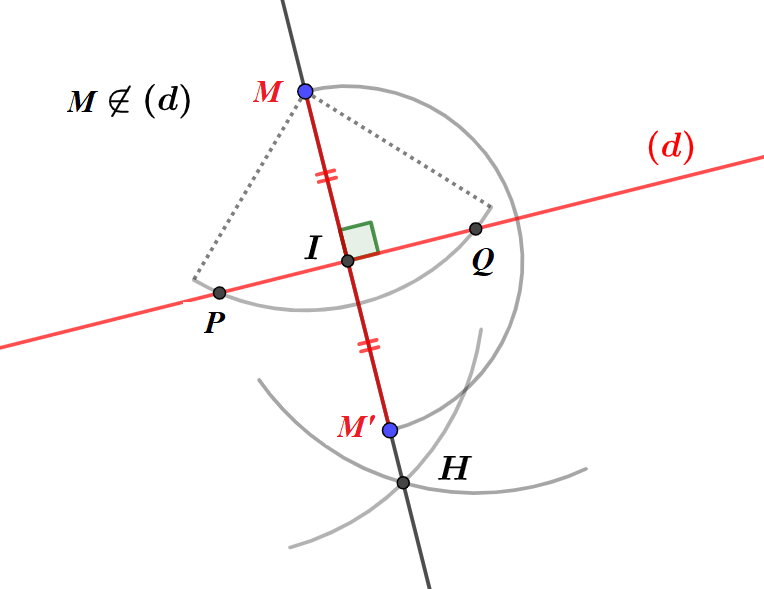
- Construire la droite $(d)$ et placer un point $M$ n’appartenant à la droite $(d)$.
- Placer la pointe sèche du compas sur le point $M$ et tracer un arc de cercle qui coupe $(d)$ en deux points $P$ et $Q$.
- A partir de $P$ et de $Q$ construire deux arcs de cercle de même rayon. Ils se coupent en un point $H$.
- La droite $(MH)$ ainsi construite est la perpendiculaire à $(d)$ passant par $M$.
- La droite $(MH)$ coupe $(d)$ en un point $I$.
- Finalement, à partir de $I$, construire un demi-cercle qui passe par $M$. Ce demi-cercle coupe $(MH)$ en $M’$.
- $M’$ est le symétrique de $M$ par rapport à la droite $(d)$. CQFD.$\blacktriangle$
2.4. Construction du symétrique d’un segment
Propriété n°1.
Le symétrique d’un segment par rapport à une droite est un segment de même longueur.
Soit $[AB]$ un segment et $\Delta$ une droite.
Pour construire le symétrique du segment $[AB]$ par rapport à la droite $\Delta$, il suffit de construire le symétrique $A’$ de $A$ et le symétrique $B’$ de $B$ par rapport à la droite $\Delta$ par la méthode de votre choix. Alors, le symétrique du segment $[AB]$ par rapport à la droite $\Delta$, est le segment $[A’B’]$ avec $$\boxed{~A’B’=AB~}$$
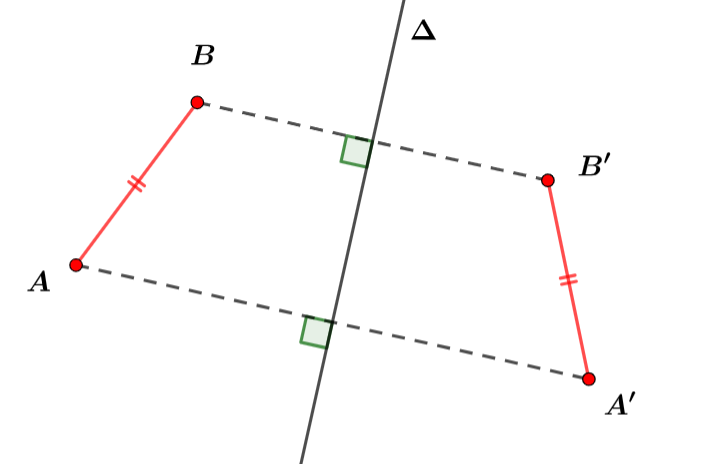
$[A’B’]$ symétrique de $[AB]$ par rapport à la droite $\Delta$
Construction du symétrique d’une figure géométrique
Pour construire le symétrique d’une figure géométrique, il suffit de construire le symétrique de chaque point remarquable de cette figure, puis relier les extrémités des segments, et compléter la figure.
Deux figures symétriques par rapport à un axe $\Delta$ sont superposables.
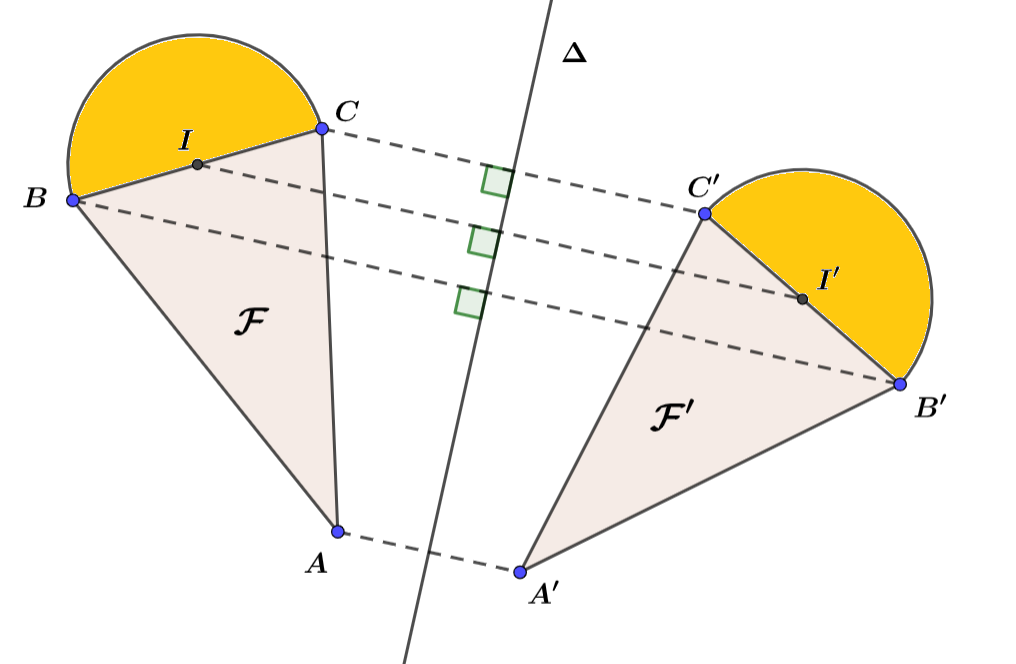
$\mathcal F’$ est le symétrique de $\mathcal F’$ par rapport à l’axe $\Delta$
3. Exercices résolus
Exercice résolu n°1.
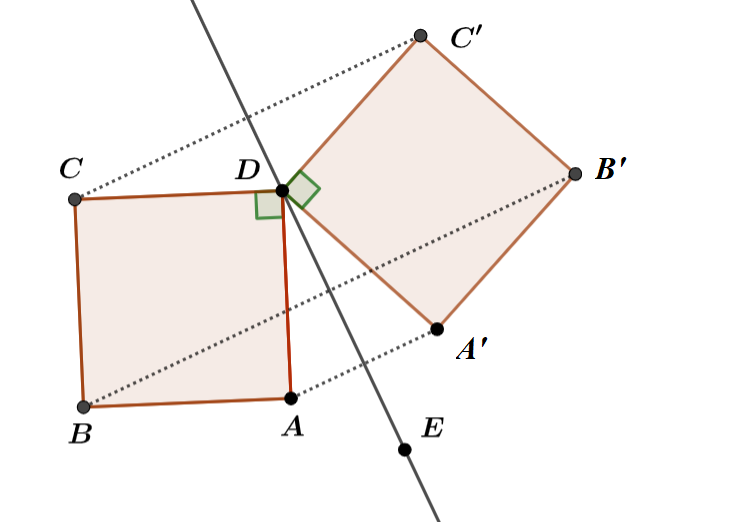
Construire un carré $ABCD$ de côté 4cm. Et placer un pont $E$ à l’extérieur du carré tel que la droite $(DE)$ ne coupe pas le carré $ABCD$. Construire le symétrique de $ABCD$ par rapport à l’axe $(DE)$.
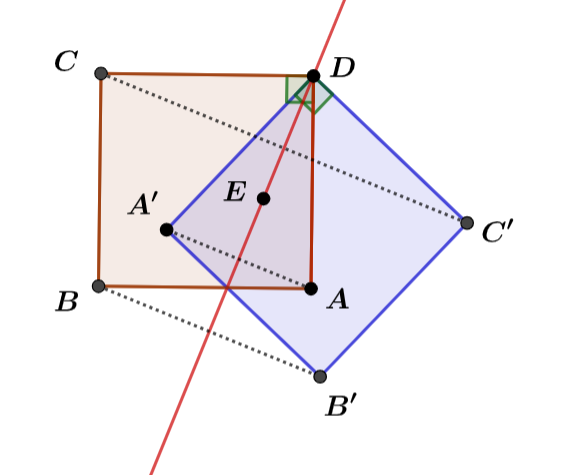
Exercice résolu n°1.
Construire un carré $ABCD$ de côté 4cm. Et placer un pont $E$ à l’intérieur du carré $ABCD$. La droite $(DE)$ traverse le carré $ABCD$. Construire le symétrique de $ABCD$ par rapport à l’axe $(DE)$.