1. Une double symétrie axiale
Construire deux droites $(d_1)$ et $(d_2)$ perpendiculaires en un point $O$.
La figure $\mathcal F_1$ est le triangle rectangle jaune.
Construire la figure $\mathcal F_2$, symétrique de la figure $\mathcal F_1$ par par rapport à la droite $d_1$. Ces deux figures sont « opposées »
Construire la figure $\mathcal F_3$, symétrique de la figure $\mathcal F_2$ par par rapport à la droite $d_2$. Ces deux figures sont également « opposées ».
Que peut-on dire des deux figures $\mathcal F_1$ et $\mathcal F_3$ ?
Sont-elles symétriques ? opposées ? ou bien « opposées et inversées » ?
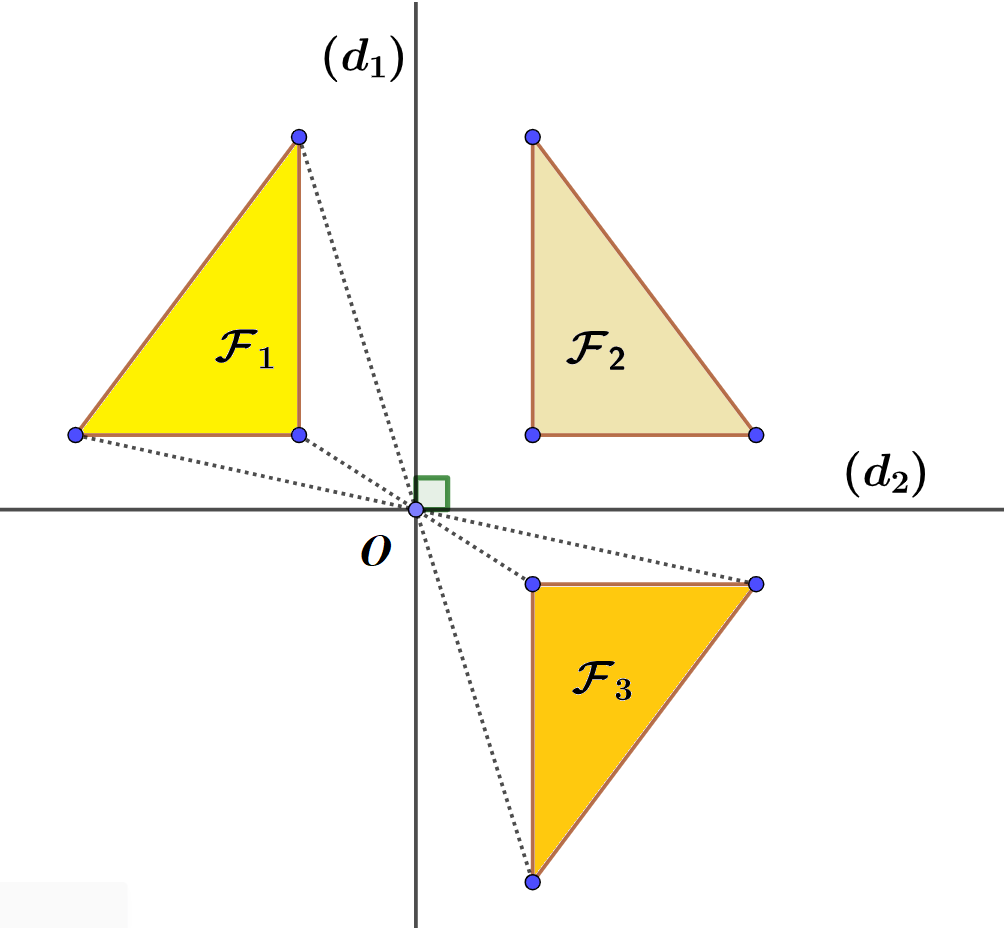
La symétrie centrale = Une double symétrie axiale
Il est clair les deux figures $\mathcal F_1$ et $\mathcal F_3$ sont symétriques, mais pas par rapport à une droite. Elles sont « superposables, opposées et inversées ». Donc, elles sont symétriques par rapport à un point, le point $O$. On dit symétrique par rapport au centre $O$.
Définition. Construction du symétrique d’un point
2.1. Définition de la symétrie centrale
Définitions 1.
On se donne deux points $O$ et $M$ du plan.
On dit que le point $M’$ est le symétrique de $M$ par rapport au point $O$, lorsque $O$ est le milieu du segment $[MM’]$.
On dit aussi que les points $M$ et $M’$ sont symétriques par rapport au centre $O$.
Une symétrie par rapport à un point $O$ s’appelle la symétrie centrale de centre $O$.
On dit aussi que $M’$ est l’image de $M$ par la symétrie centrale de centre $O$.
Remarques importantes
1°) Si $M’$ est le symétrique de $M$ par rapport au centre $O$, alors $M$ est le symétrique de $M’$ par rapport au centre $O$. On dit aussi que les points $M$ et $M’$ sont symétriques par rapport au centre $O$.
2°) Si $M’$ est le symétrique de $M$ par rapport au centre $O$, alors les trois points $M$, $O$ et $M’$ sont alignés dans cet ordre et on a : $$\boxed{~OM’=OM~}$$
3°) Dans une symétrie centrale de centre $O$, le seul point qui a pour symétrique lui-même est le point $O$. On dit que le point $O$ est invariant par la symétrie de centre $O$.
$O$ s’appelle aussi le centre de symétrie.
2.2. Construction du symétrique d’un point
a) Construction du symétrique d’un point à la règle uniquement
- Placer les deux points $O$ et $M$ dans le plan.
- Tracer la demi-droite d’origine $M$ passant par $O$ et la prolonger.
- Placer le point $M’$ sur la demi-droite $[MO)$ tel que : $$\boxed{~OM’=OM~}$$
- $M’$ est le symétrique de $M$ par rapport au centre $O$. CQFD.$\blacktriangle$
b) Construction du symétrique d’un point à la règle et au compas
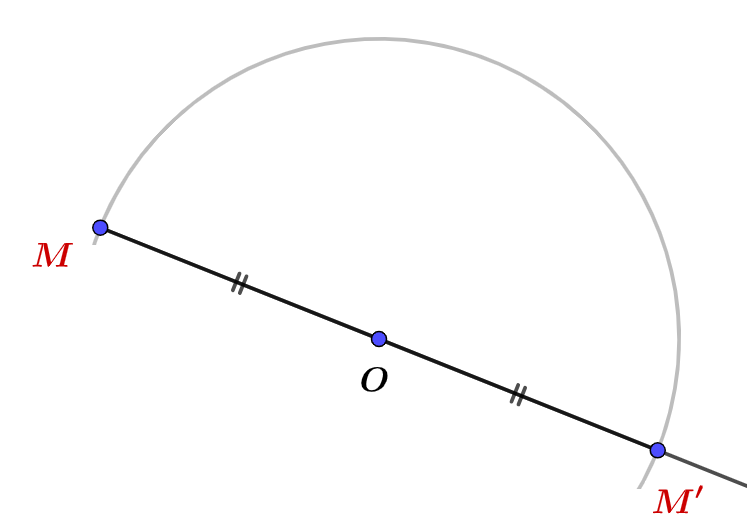
- Placer les deux points $O$ et $M$ dans le plan.
- Construire un demi-cercle de centre $O$ et passant par $M$.
- Ce demi-cercle coupe la demi-droite $[MO)$ en un point $M’$.
- $M’$ est le symétrique de $M$ par rapport au centre $O$ et on a : $$\boxed{~OM’=OM~}$$ CQFD.$\blacktriangle$
3. Exercices résolus
Exercice résolu n°1.
Refaites les deux constructions ci dessus.
