« Une figure bien faite et bien codée est un problème à moitié résolu » Albert EINSTEIN.

Très souvent, pour faire un exercice de géométrie et illustrer le problème, je dois faire une figure (à main levée si ce n’est pas demandé) et « coder la figure » pour visualiser les données sur la figure et trouver visuellement les propriétés que je dois utiliser pour résoudre le problème.

Inversement, si une figure codée est donnée dans l’exercice. Je dois « décoder la figure » et analyser toutes les informations qu’elle indique d’une manière directe ou indirecte. L’objectif étant aussi de trouver visuellement les propriétés que je dois utiliser pour résoudre le problème.

1. Coder une figure géométrique

Coder une figure c’est mettre le même symbole sur les segments ayant la même longueur ou les angles de même mesure et indiquer les longueurs ou mesures données. Ce qui revient à reporter sur la figure les informations données dans l’énoncé.

Figure 1.

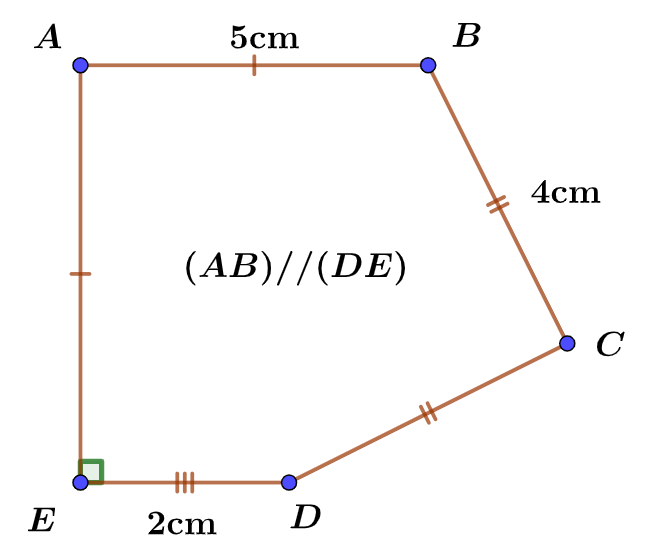
1.1. Cotés de même longueur

Propriété n°1.
On utilise le même codage pour des côtés de même longueur.

Les cotés $[AB]$ et $[AE]$ sont codés par un trait. Ils ont la même longueur. Donc : $$\boxed{~AE=AB=5cm~}$$ De même, les cotés $[BC]$ et $[CD]$ sont codés par un double-trait. Ils ont la même longueur. Donc : $$\boxed{~BC=CD=4cm~}$$ Le côté $[ED]$ est codé par un triple-trait. Il est le seul. Donc, sa longueur est différente des autres.

On remarque également que $\widehat{AED}$ est un angle droit.
Et on a indiqué que $(AB)//(DE)$. Donc les droites $(AB)$ et $(DE)$ sont parallèles.

1.2. Angles de même mesure

Figure 2.

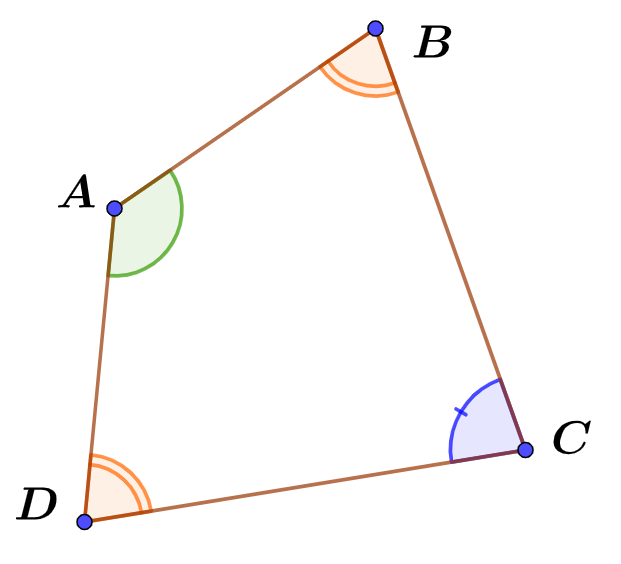
Propriété n°2.
On utilise le même codage pour les angles (égaux ou) de même mesure.

Comme pour les longueurs des côtés, les angles (égaux ou) de même mesure sont indiqués par le même codage.
Ici, on voit que : $$\boxed{~\widehat{ABC}=\widehat{ADC}~}$$

1.3. Codage d’un cercle

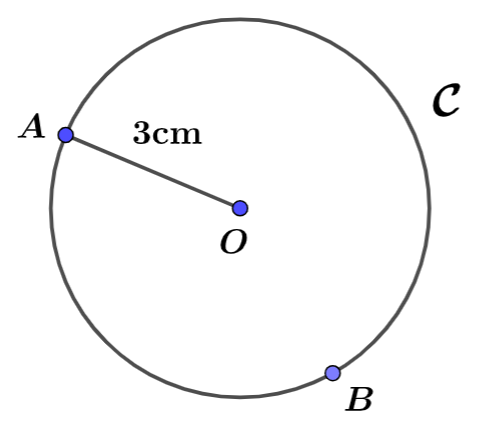
Propriété n°3.
Pour coder un cercle, on doit indiquer le centre $O$ et le rayon $r$ du cercle ${\mathcal C}$.

Pour cela, on place un point $A$ quelconque (ou précis) sur le cercle et indiquer que $OA=r$.
En général, le cercle de centre $O$ et le rayon $r$, se note ${\mathcal C}(O;r)$.

Figure 3. Cercle ${\mathcal C}(O;3cm)$ de centre $O$ et de rayon $r=3$cm.

2. Décodage d’une figure géométrique

2.1 Différentes lectures de la figure 1.

Dans la figure 1, on peut d’ores et déjà tirer plusieurs conséquences.

  1. $\widehat{AED}$ est un angle droit.
    Donc : $\widehat{AED}=90°$ et les droites $(AE)$ et $(ED)$ sont perpendiculaires
  2. Les droites $(AB)$ et $(DE)$ sont parallèles et les droites $(AE)$ et $(ED)$ sont perpendiculaires.
    Donc, grâce à une propriété de 6ème, on pourrait en déduire que « les droites $(AE)$ et $(AB)$ sont perpendiculaires ». Et par suite que $\widehat{EAB}=90°$.
  3. $AB=AE$ et $\widehat{EAB}=90°$, donc le triangle $ABE$ est isocèle rectangle en $A$.
  4. $BC=CD$, donc le triangle $BCD$ est isocèle en $C$.

2.2 Différentes lectures de la figure 2.

Dans la figure 2, $ABCD$ est un quadrilatère avec deux angles (égaux ou) de même mesure. $$\boxed{~\widehat{ABC}=\widehat{ADC}~}$$

2.2 Différentes lectures de la figure 3.

Dans la figure 3, ${\mathcal C}$ est le cercle de centre $O$ et le rayon $r$. On voit que $A\in{\mathcal C}(O;3cm)$ et $B\in{\mathcal C}(O;3cm)$. Donc $OA=OB=rayon$. D’où $OA=OB=3$cm.

3. Exercices résolus

Exercice résolu n°1.


CQFD $\blacktriangle$