1. Angles opposés par le sommet. Définition, propriétés

Définition 1.
On dit que deux angles sont opposés par le sommet, lorsque :
$\quad$1°) Ils ont le même sommet ;
$\quad$2°) Leurs côtés sont situés dans le prolongement l’un de l’autre.

Illustration :
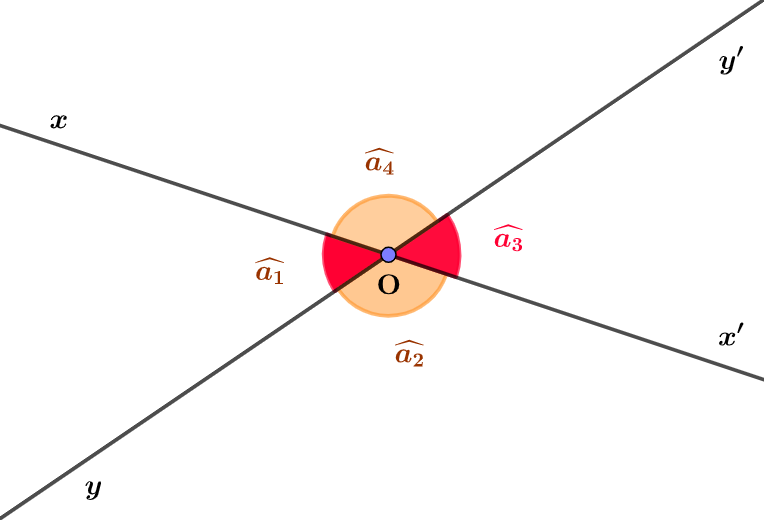
Si les deux droites $(xx’)$ et $(yy’)$ sont sécantes en un point $O$, alors
les deux angles $\widehat{a_1}=\widehat{xOy}$ et $\widehat{a_3}=\widehat{x’Oy’}$ sont angles opposés par le sommet
Et les deux angles $\widehat{a_2}=\widehat{x’Oy}$ et $\widehat{a_4}=\widehat{xOy’}$ sont angles opposés par le sommet.

Figure 1.
Angles opposés par le sommet
Figure 2. Symétries des angles opposés par le sommet

Propriété fondamentale n°1.
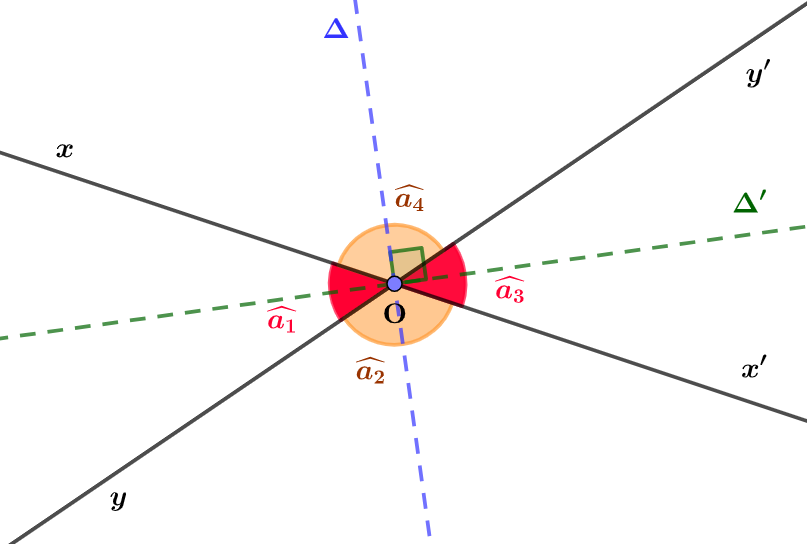
Deux angles opposés par le sommet ont trois éléments de symétrie :
– Les deux bissectrices $\Delta$ et $\Delta’$ des deux angles sont deux axes de symétrie.
– Le sommet $O$ est un centre de symétrie.

Propriété fondamentale n°2.
Deux angles opposés par le sommet sont symétriques, donc ils sont de même mesure. $$\boxed{~\widehat{a_1}=\widehat{a_3}~}~~\text{et}~~\boxed{~\widehat{a_2}=\widehat{a_4}~}$$

3. Exercices résolus

Exercice résolu n°1.
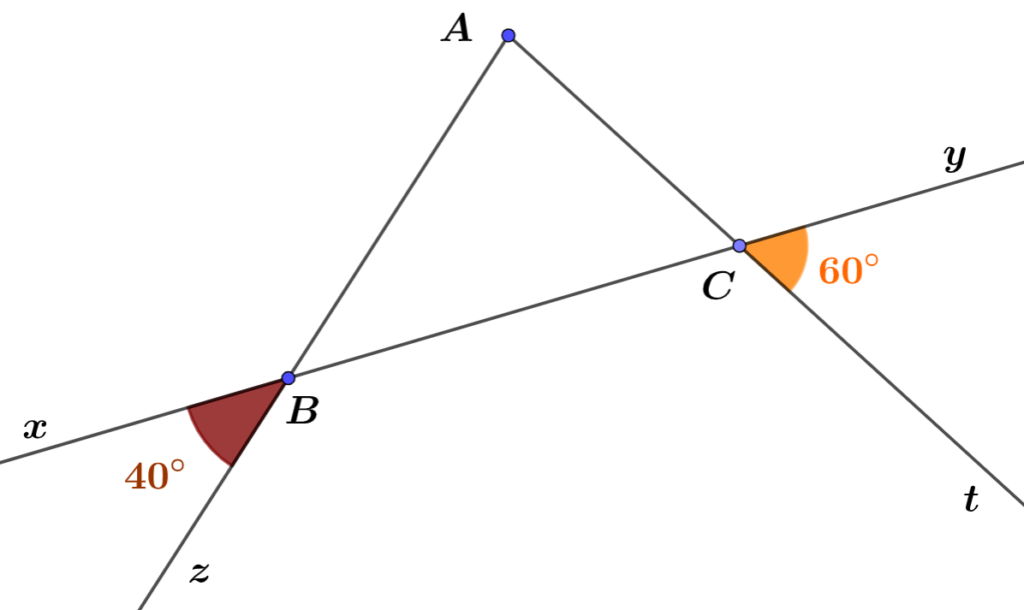
Dans la figure 4 ci-dessous, calculer les mesure des angles du triangle $ABC$.

1°) Calcul de $\widehat{ABC}$.
On sait que la mesure de l’angle $\widehat{xBz}=40°$ et les angles $\widehat{xBz}$ et $\widehat{ABC}$ sont opposés par le sommet.
Or, d’après le cours : « Si deux angles sont opposés par le sommet, alors ils sont de même mesure ».
Donc : $\widehat{ABC}=\widehat{xBz}$. Ce qui donne : $$\boxed{~\widehat{ABC}=40^\circ~}$$

2°) Calcul de $\widehat{ACB}$.
On sait que la mesure de l’angle $\widehat{yCt}=60°$ et les angles $\widehat{yCt}$ et $\widehat{ACB}$ sont opposés par le sommet.
Or, d’après le cours : « Si deux angles sont opposés par le sommet, alors ils sont de même mesure ».
Donc : $\widehat{ACB}=\widehat{yCt}$. Ce qui donne : $$\boxed{~\widehat{ACB}=60^\circ~}$$

3°) Calcul de $\widehat{BAC}$.
D’après ce qui précède, on sait que $\widehat{ABC}=40°$ et $\widehat{ACB}=60°$.
Or, d’après le cours : « Dans un triangle quelconque, la somme des mesures des trois angles est égale à $180°$ ».
Donc : $$\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180°$$ Ce qui donne : $$40°+60°+\widehat{BAC}=180°$$ ou encore : $$100°+\widehat{BAC}=180°$$
Finalement, par soustraction, on obtient $$\widehat{BAC}=180°-100°$$
Conclusion. $$\boxed{~\widehat{BAC}=80^\circ~}$$
CQFD $\blacktriangle$

Exercice résolu n°2.
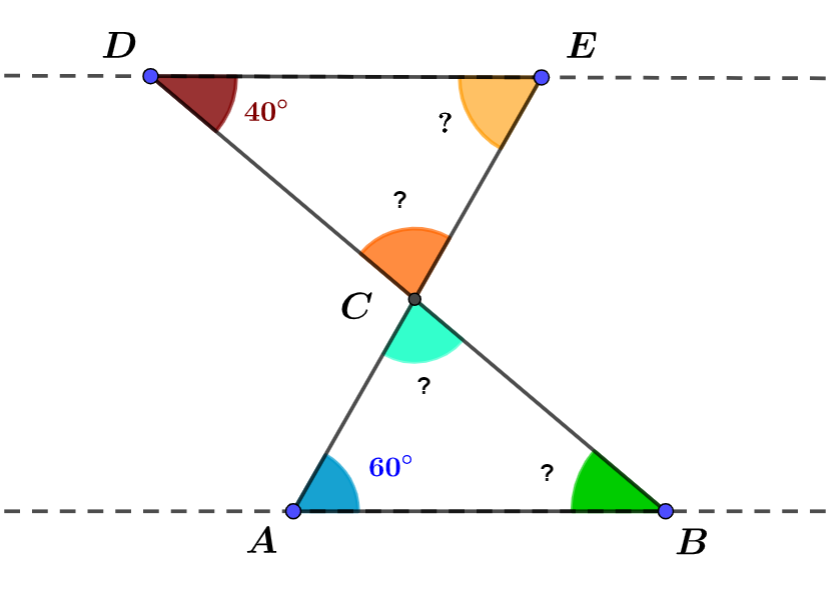
Dans la figure ci-dessous, les droites $(AB)$ et $(DE)$ sont parallèles et les droites $(AE)$ et $(BD)$ sont sécantes en $C$.
1°) Calculer les mesures des angles du triangle $ABC$.
2°) Calculer les mesures des angles du triangle $CDE$.

Figure 5.

1°) Calculer les mesures des angles du triangle $ABC$.
a) Calcul de $\widehat{ABC}$.
On sait que $\boxed{~\widehat{BAC}=40°~}$ et les droites $(AB)$ et $(DE)$ sont parallèles et coupées par la sécante $(BD)$. Donc, les angles $\widehat{ABC}$ et $\widehat{CDE}$ sont alternes-internes.
Or, d’après le cours, « Si deux droites sont parallèles et coupées par une sécante, alors les angles alternes-internes qu’elles forment sont de même mesure ». Donc, $\widehat{ABC}=\widehat{CDE}$.
Conclusion. $$\boxed{~\widehat{ABC}=40°~}$$
b) Calcul de $\widehat{ACB}$.
D’après ce qui précède, on sait que $\widehat{BAC}=60°$ et $\widehat{ABC}=40°$.
Or, d’après le cours : « Dans un triangle quelconque, la somme des mesures des trois angles est égale à $180°$ ».
Donc : $$\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180°$$ Ce qui donne : $$60°+40°+\widehat{ACB}=180°$$ ou encore : $$100°+\widehat{ACB}=180°$$
Finalement, par soustraction, on obtient $$\widehat{ACB}=180°-100°$$ Conclusion. $$\boxed{~\widehat{ACB}=80^\circ~}$$


2°) Calculer les mesures des angles du triangle $CDE$.
D’une manière analogue on démontre que les angles $\widehat{BAC}$ et $\widehat{CED}$ sont alternes-internes. Donc : $$\boxed{~\widehat{CED}=60°~}$$
D’autre part, on sait que la mesure de l’angle $\widehat{ACB}=80°$ et les angles $\widehat{ACB}$ et $\widehat{DCE}$ sont opposés par le sommet.
Or, d’après le cours : « Si deux angles sont opposés par le sommet, alors ils sont de même mesure ».
Donc : $\widehat{DCE}=\widehat{ACB}$. Ce qui donne : $$\boxed{~\widehat{DCE}=80^\circ~}$$ CQFD $\blacktriangle$