1. Angles correspondants. Définition, propriétés
Définition 1. (Figure 1.)
Soient $(d_1)$ et $(d_2)$ deux droites coupées par une droite sécante $\Delta$ en deux points $A$ et $B$ respectivement.
On appelle angles correspondants, deux angles non adjacents situés du même côté de la sécante $\Delta$, l’un est situé entre les droites $(d_1)$ et $(d_2)$ et l’autre non.
Autrement dit
On appelle angles correspondants, deux angles non adjacents situés du même côté de la sécante $\Delta$, tous les deux sont situés en dessous ou tous les deux situés au-dessus des droites $(d_1)$ et $(d_2)$.
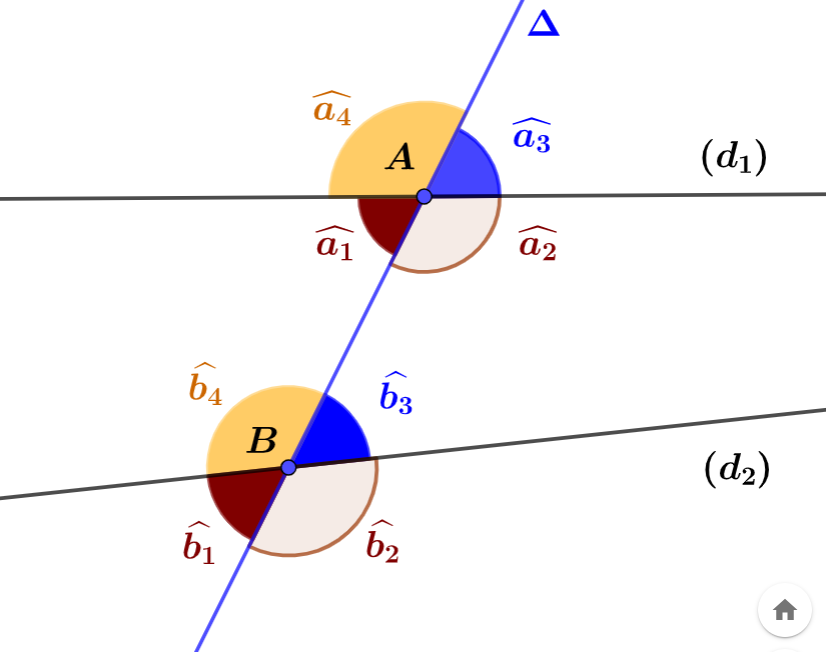
Les angles de même couleur sont correspondants
Exemples
Dans la figure 1 ci-dessus, les angles $\widehat{a_1}$ et $\widehat{b_1}$ sont des angles correspondants.
De même, les angles $\widehat{a_2}$ et $\widehat{b_2}$ sont des angles correspondants.
les angles $\widehat{a_3}$ et $\widehat{b_3}$ sont des angles correspondants.
les angles $\widehat{a_4}$ et $\widehat{b_4}$ sont des angles correspondants.
Propriété fondamentale n°1. (Figure 2.)
Si deux droites $(d_1)$ et $(d_2)$ sont parallèles et coupées par une droite sécante $\Delta$ en deux points $A$ et $B$ respectivement, alors les angles correspondants qu’elles forment sont de même mesure.
$\boxed{~\widehat{a_1}=\widehat{b_1}}$ et $\boxed{~\widehat{a_2}=\widehat{b_2}~}$ et $\boxed{~\widehat{a_3}=\widehat{b_3}~}$ et $\boxed{~\widehat{a_4}=\widehat{b_4}~}$.
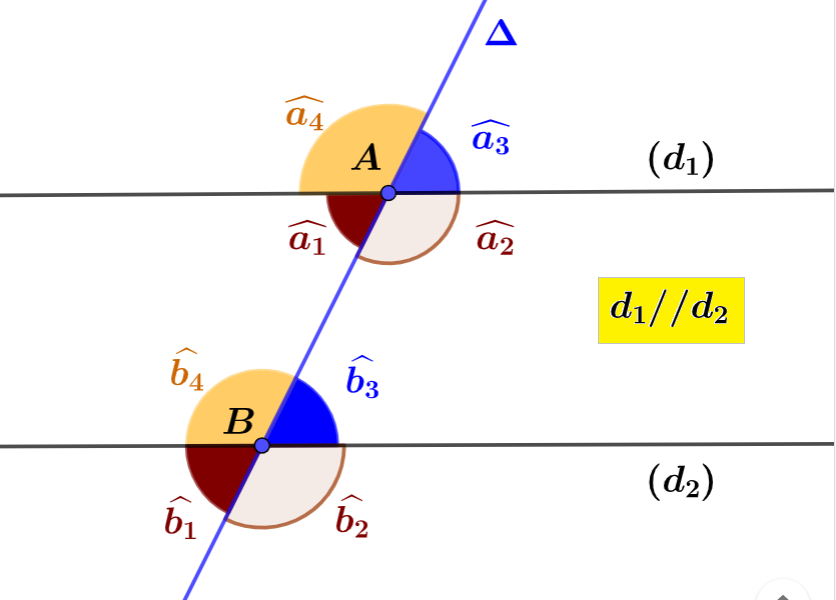
Si $d_1//d_2$, alors les angles de même couleur sont correspondants et de même mesure
3. Exercices résolus
Exercice résolu n°1.
On utilise les éléments de la figure 2, où $d_1//d_2$ avec $\widehat{a_1}=48°$.
1°) Déterminer la mesure de l’angle $\widehat{b_1}$.
2°) En déduire la mesure des angles $\widehat{b_2}$ et $\widehat{b_3}$.
