1. Angles complémentaires
Définition 1.
Deux angles $\widehat{a}$ et $\widehat{b}$ sont dits complémentaires lorsque, en les juxtaposant, on obtient un angle droit.
Autrement dit : Deux angles sont complémentaires si la somme de leurs mesures est égale à $90^\circ$ : $$\boxed{~\widehat{a}+\widehat{\,b\,}=90^\circ~}$$
Exemples
1°) Les deux angles $\widehat{a}=35^\circ$ et $\widehat{\,b\,}=55^\circ$ sont-ils complémentaires ?
2°) Les deux angles $\widehat{\,c\,}=37^\circ$ et $\widehat{d}=63^\circ$ sont-ils complémentaires ?
1°) Les deux angles $\widehat{a}=35^\circ$ et $\widehat{\,b\,}=55^\circ$ sont complémentaires car : $$\widehat{a}+\widehat{\,b\,}=35^\circ+55^\circ=90^\circ$$
2°) Les deux angles $\widehat{\,c\,}=37^\circ$ et $\widehat{d}=63^\circ$ ne sont pas complémentaires car : $$\widehat{\,c\,}+\widehat{d}=37^\circ+67^\circ=100^\circ\not=90^\circ.$$
Propriété 2.
Dans un triangle $ABC$ rectangle en $A$, les deux angles aigus $\widehat{B}$ et $\widehat{C}$ sont complémentaires. $$\boxed{~\widehat{B}+\widehat{C}=90^\circ~}$$
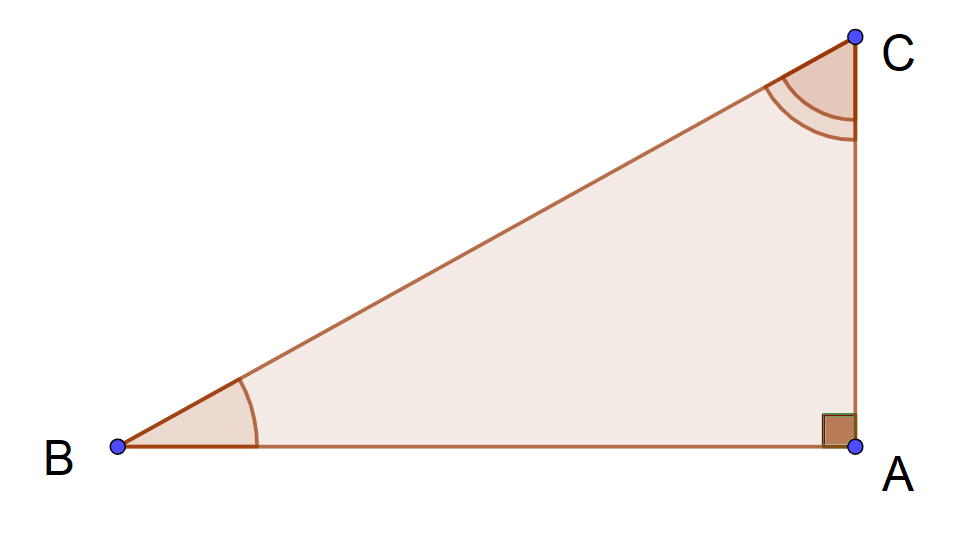
Ses deux angles aigus $\widehat{B}$ et $\widehat{C}$ sont complémentaires.
2. Angles supplémentaires
Définition 2.
Deux angles $\widehat{a}$ et $\widehat{\,b\,}$ sont dits supplémentaires lorsque, en les juxtaposant, on obtient un angle plat.
Autrement dit : Deux angles $\widehat{a}$ et $\widehat{\,b\,}$ sont dits supplémentaires si la somme de leurs mesures est égale à $180^\circ$ : $$\boxed{~\widehat{a}+\widehat{b}=180^\circ~}$$
(AB) est une droite. Les trois points $B$, $A$ et $C$ sont alignés. Ils forment un angle plat.
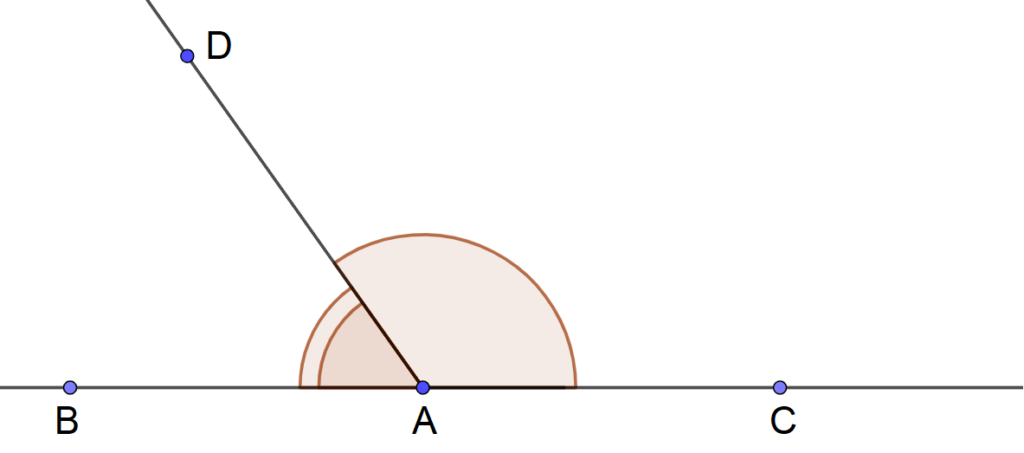
Exemples
1°) Les angles $\widehat{a}=115^\circ$ et $\widehat{\,b\,}=65^\circ$ sont-ils supplémentaires ?
1°) Les angles $\widehat{\,c\,}=139^\circ$ et $\widehat{d}=51^\circ$ sont-ils supplémentaires ?
1°) Les deux angles $\widehat{a}=115^\circ$ et $\widehat{\,b\,}=65^\circ$ sont supplémentaires car : $$\widehat{a}+\widehat{\,b\,}=115^\circ+65^\circ=180^\circ$$
2°) Les deux angles $\widehat{\,c\,}=139^\circ$ et $\widehat{d}=51^\circ$ ne sont pas supplémentaires car : $$\widehat{\,c\,}+\widehat{d}=115^\circ+51^\circ=190^\circ\not=180^\circ.$$
Propriété 3.
Dans un parallélogramme, les angles consécutifs sont supplémentaires.
Démonstration
Voir chapitre sur les angles alternes internes
ou chapitre sur le parallélogramme.
Exercices résolus
Exercice résolu n°1.
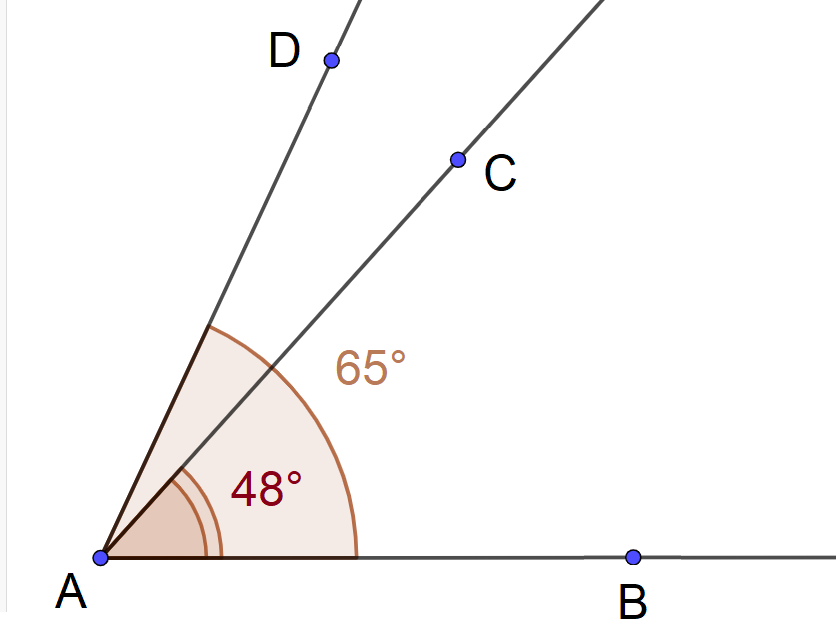
1°) Construire les deux angles suivants placés du même côté de $[AB)$ tels que $\widehat{BAC}=48^\circ$ et $\widehat{BAD}=65^\circ$.
2°) Calculer la mesure de l’angle : $\widehat{CAD}$.
1°) Construction de la figure :
2°) Calculer la mesure de l’angle : $\widehat{CAD}$.
Les deux angles $\widehat{BAC}$ et $\widehat{BAD}$ ont le même sommet $A$, un côté commun $[AB)$, mais ne sont pas situés de part et d’autre de ce côté commun. Donc ils ne sont pas adjacents.
Par contre, par construction, les deux angles $\widehat{BAC}$ et $\widehat{CAD}$ ont le même sommet $A$, un côté commun $[AC)$ et sont situés de part et d’autre de ce côté commun. Donc ils sont adjacents.
Donc, la mesure du grand angle $\widehat{BAD}$ est égale à la somme des mesures des deux angles qui le composent. Ce qui donne : $$\widehat{BAD}=\widehat{BAC}+\widehat{CAD}$$ Ce qui donne : $$65^\circ=48^\circ+\widehat{CAD}$$ Et par soustraction, on obtient : $$\widehat{CAD}=65^\circ-48^\circ=17^\circ$$
Conclusion. $$\boxed{~\widehat{CAD}=17^\circ~}$$
Exercice résolu n°2.
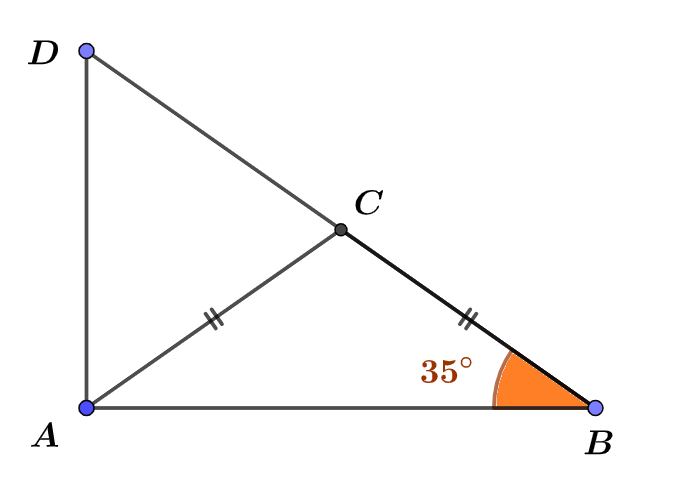
Construire un triangle $ABD$ rectangle en $A$ et tel que $AB=10$ cm et $\widehat{ABD}=35°$.
Placer le point $C$ sur le côté $[AB]$ tel que $ABC$ soit un triangle isocèle en $C$. Toutes les réponses doivent être justifiées.
1°) Faire une figure.
2°) Déterminer la mesure de l’angle : $\widehat{BAC}$.
3°) Calculer la mesure de l’angle : $\widehat{ACB}$.
4°) Calculer la mesure de l’angle : $\widehat{ACD}$.
5°) Calculer la mesure de l’angle : $\widehat{CAD}$.
6°) Calculer la mesure de l’angle : $\widehat{ADB}$.
1°) Construction de la figure :
2°) Déterminer la mesure de l’angle : $\widehat{BAC}$.
D’une part, on sait que, dans le triangle $ABC$ : $\widehat{ABC}=35°$.
D’autre part, le triangle $ABC$ est isocèle en $C$. Donc, ses deux angles à la base sont de même mesure. Donc : $\widehat{BAC}=\widehat{ABC}$.
Par conséquent : $\boxed{~\widehat{BAC}=35^\circ~}$
3°) Calculer la mesure de l’angle : $\widehat{ACB}$.
On sait que, dans le triangle $ABC$ : $\widehat{ABD}=35°$ et $\widehat{ABC}=35°$.
Or, « Dans un triangle quelconque, la somme des mesures des trois angles est égale à 180° ». Donc : $\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180°$
Ce qui donne : $\widehat{ACB}+35°+35°=180°$$
Ou encore : $\widehat{ACB}+70°=180°$
Et par soustraction, on obtient : $\widehat{ACB}=180°-70°$
Conclusion. $\boxed{~\widehat{ACB}=110^\circ~}$
4°) Calculer la mesure de l’angle : $\widehat{ACD}$.
On sait que, les deux angles $\widehat{ACB}$ et $\widehat{ACD}$ sont adjacents et forment un angle plat. Ils sont supplémentaires.
Donc : $\widehat{ACB}+\widehat{ACD}=180°$
Ce qui donne : $110°+\widehat{ACD}=180°$
Et par soustraction, on obtient : $\widehat{ACD}=180°-110°$
Conclusion. $\boxed{~\widehat{ACD}=70^\circ~}$
5°) Calculer la mesure de l’angle : $\widehat{CAD}$.
On sait que, les deux angles $\widehat{CAB}$ et $\widehat{CAD}$ sont adjacents et forment un angle droit. Ils sont complémentaires.
Donc : $\widehat{CAB}+\widehat{CAD}=90°$
Ce qui donne : $35°+\widehat{CAD}=90°$
Et par soustraction, on obtient : $\widehat{CAD}=90°-35°$
Conclusion. $\boxed{~\widehat{CAD}=55^\circ~}$
6°) Calculer la mesure de l’angle : $\widehat{ADB}$.
On sait que, le triangle $ABD$ est rectangle en $A$ et $\widehat{ABD}=35°$.
Or, « Dans un triangle rectangle, les deux angles aigus sont complémentaires »
Donc : $\widehat{ABD}+\widehat{ADB}=90°$
Ce qui donne : $35°+\widehat{ADB}=90°$
Et par soustraction, on obtient : $\widehat{ADB}=90°-35°$
Conclusion. $\boxed{~\widehat{ADB}=55^\circ~}$.