1. Angles alternes internes. Définition, propriétés

On trouve le mot « alternes » ou « alternées » en botanique concernant la disposition des feuilles sur une tige. Nous rencontrons plusieurs possibilités. Les deux cas qui nous intéressent que nous utiliserons pour les angles, sont :

  • les « feuilles alternées » disposées sur l’axe de la tige de façon isolée, alternativement de part et d’autre de l’axe.
  • et es « feuilles opposées » disposées sur l’axe de la tige de façon symétrique de part et d’autre de l’axe.
Figure 1.
feuilles opposées $\quad$ et $\quad$ feuilles alternées

Si deux droites $(d_1)$ et $(d_2)$ forment une bande. On dira que des angles sont « internes » s’ils sont situés à l’intérieur de la bande et « externes » s’ils sont situés à l’extérieur.

Définition 1.
Soient $(d_1)$ et $(d_2)$ deux droites parallèles, et soit $\Delta$ une droite sécante qui coupe $(d_1)$ et $(d_2)$ en deux points $A$ et $B$ respectivement (Figure 1).
On appelle angles alternes-internes, deux angles non adjacents situés entre les deux droites parallèles $(d_1)$ et $(d_2)$ et de part et d’autre de la sécante $\Delta$.

Figure 2.
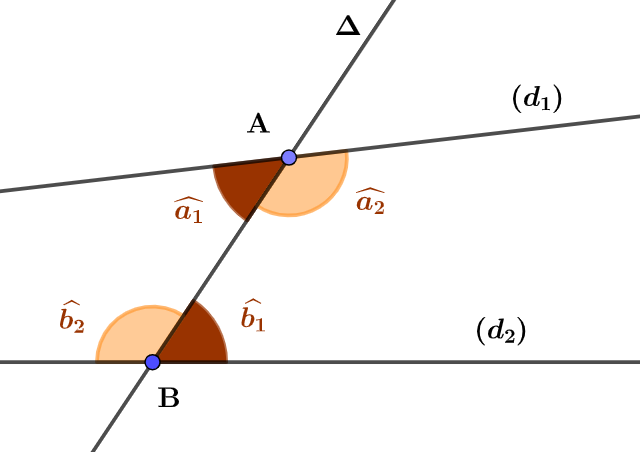
Les angles de même couleur sont alternes-internes

Exemples

Dans la figure 2 ci-dessus, les angles $\widehat{a_1}$ et $\widehat{b_1}$ sont des angles alternes-internes.
De même, les angles $\widehat{a_2}$ et $\widehat{b_2}$ sont des angles alternes-internes.

Propriété fondamentale n°1.
Si deux droites $(d_1)$ et $(d_2)$ sont parallèles et coupées par une droite sécante $\Delta$ en deux points $A$ et $B$ respectivement (Figure 3), alors les angles alternes-internes qu’elles forment sont de même mesure.$$\boxed{~\widehat{a_1}=\widehat{b_1}~}~~\text{et}~~\boxed{~\widehat{a_2}=\widehat{b_2}~}$$

Figure 3.
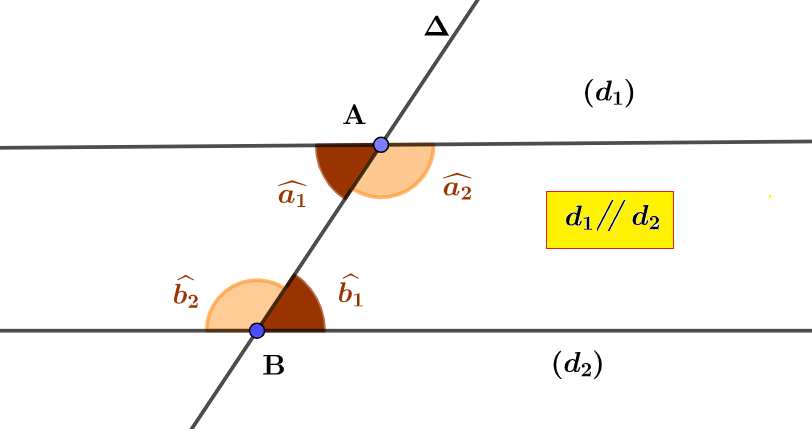
Droites parallèles et angles alternes-internes

2. Application dans un parallélogramme

Propriété fondamentale n°2.
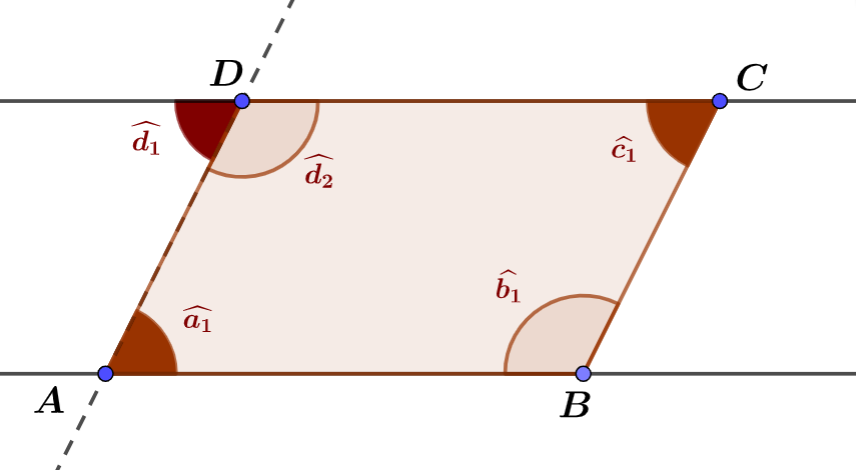
Dans un parallélogramme $ABCD$ quelconque,
1°) Les angles consécutifs sont supplémentaires. $$\boxed{~\widehat{BAD}+\widehat{ADC}=180^\circ~}$$
2°) Les angles opposés sont de même mesure. $$\boxed{~\widehat{BAD}=\widehat{BCD}~}$$

Cette propriété est très importante et permet de calculer les mesures des angles dans beaucoup de situations en Géométrie.

On fait d’abord une figure. Voir ci-dessus.
1°) Montrons que les angles consécutifs sont supplémentaires. $$\boxed{~\widehat{BAD}+\widehat{ADC}=180^\circ~}$$

On sait que Les droites $(AB)$ et $(DC)$ sont parallèles et coupées par la droite sécante $(AD)$ en $A$ et $D$.
Donc, les deux angles $\widehat{a_1}$ et $\widehat{d_1}$ sont alternes-internes.
Or, d’après le cours : « Si deux droites sont parallèles et coupées par une sécante, alors les angles alternes-internes qu’elles forment sont de même mesure ».
Donc : $$\boxed{~\widehat{a_1}=\widehat{d_1}~}$$

D’autre part,
On sait que les deux angles $\widehat{d_1}$ et $\widehat{d_2}$ sont adjacents et forment un angle plat. Donc, ils sont supplémentaires. Donc : $$\boxed{~\widehat{d_1}+\widehat{d_2}=180^\circ~}$$
Donc : En remplaçant $\widehat{d_1}$ par $\widehat{a_1}$ dans l’égalité précédente, on obtient : $$\boxed{~\widehat{a_1}+\widehat{d_2}=180^\circ~}$$

On recommence de la même façon pour les autres angles.

Conclusion. Dans un parallélogramme $ABCD$ quelconque, les angles consécutifs sont supplémentaires.

2°) On sait que Les deux angles consécutifs $\widehat{a_1}$ et $\widehat{d_2}$ sont supplémentaires. Donc : $$\widehat{a_1}+\widehat{d_2}=180^\circ$$ Donc : $$\widehat{a_1}=180^\circ-\widehat{d_2}\qquad(1)$$
De même : On sait que Les deux angles consécutifs $\widehat{d_2}$ et $\widehat{c_1}$ sont supplémentaires. Donc : $$\widehat{d_2}+\widehat{c_1}=180^\circ$$ Donc : $$\widehat{c_1}=180^\circ-\widehat{d_2}\qquad(2)$$
Finalement, d’après (1) et (2), on voit bien que $$\widehat{c_1}=\widehat{a_1}$$
On en déduit que : $$\boxed{~\widehat{BAD}=\widehat{BCD}~}$$ Conclusion. Dans un parallélogramme $ABCD$ quelconque, les angles opposés sont de même mesure.
CQFD $\blacktriangle$

3. Exercices résolus

Exercice résolu n°1.
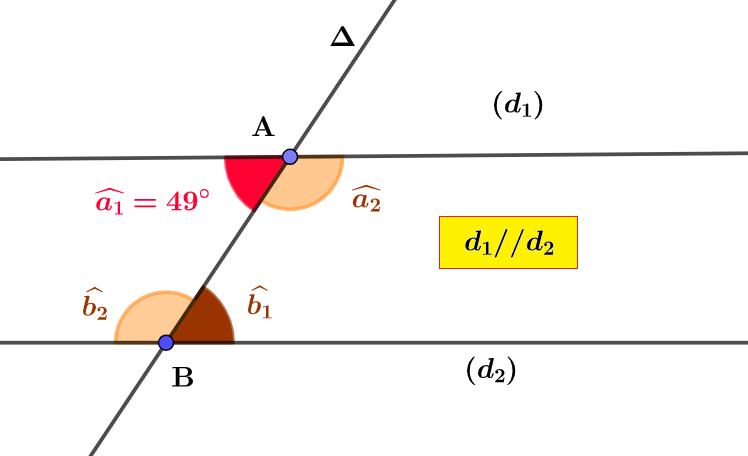
Dans la figure 4 ci-dessous, les droites $(d_1)$ et $(d_2)$ sont parallèles, et coupées par une droite sécante $\Delta$ en deux points $A$ et $B$ respectivement, avec $\widehat{a_1}=49°$.
Calculer les mesure des angles $\widehat{b_1}$, $\widehat{a_2}$ et $\widehat{b_2}$.

Figure 4.

1°) Calcul de $\widehat{b_1}$.
On sait que Les droites $(d_1)$ et $(d_2)$ sont parallèles et coupées par une droite sécante $\Delta$ en $A$ et $B$ et que $\widehat{a_1}=49°$.
Donc, les deux angles $\widehat{a_1}$ et $\widehat{b_1}$ sont alternes-internes.
Or, d’après le cours : « Si deux droites sont parallèles et coupées par une sécante, alors les angles alternes-internes qu’elles forment sont de même mesure ».
Donc : $\widehat{a_1}=\widehat{b_1}$. Ce qui donne : $$\boxed{~\widehat{b_1}=49^\circ~}$$

2°) Calcul de $\widehat{a_2}$.
On sait que les deux angles $\widehat{a_1}$ et $\widehat{a_2}$ sont adjacents et forment un angle plat. Donc, ils sont supplémentaires.
Donc : $\widehat{a_1}+\widehat{a_2}=180^\circ$.
Ou encore : $49^\circ+\widehat{a_2}=180^\circ$.
Donc : $\widehat{a_2}=180^\circ-49^\circ$.
Ce qui donne : $$\boxed{~\widehat{a_2}=131^\circ~}$$

3°) Calcul de $\widehat{b_2}$.
On sait que Les droites $(d_1)$ et $(d_2)$ sont parallèles et coupées par une droite sécante $\Delta$ en $A$ et $B$ et que $\widehat{a_2}=131^\circ$.
Donc, les deux angles $\widehat{a_2}$ et $\widehat{b_2}$ sont alternes-internes.
Or, d’après le cours : « Si deux droites sont parallèles et coupées par une sécante, alors les angles alternes-internes qu’elles forment sont de même mesure ».
Donc : $\widehat{a_2}=\widehat{b_2}$. Ce qui donne : $$\boxed{~\widehat{b_2}=131^\circ~}$$
CQFD $\blacktriangle$

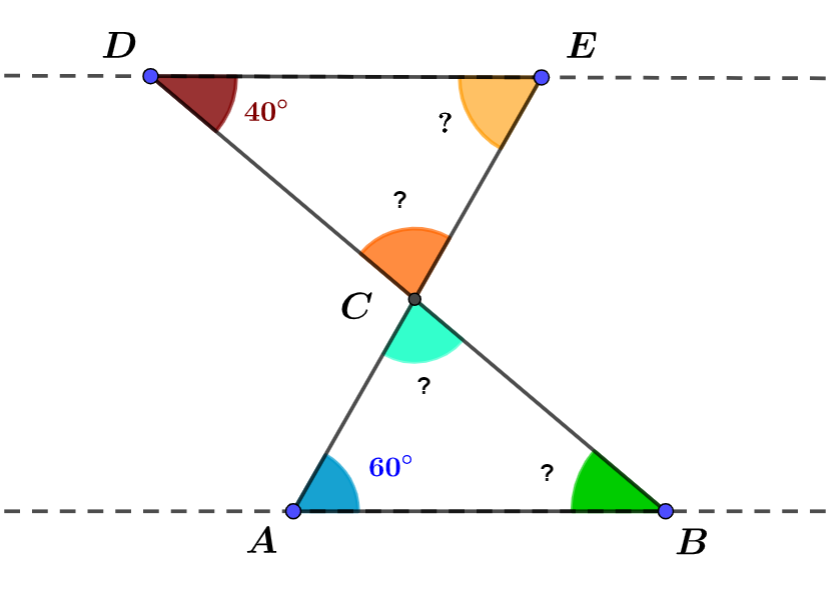
Exercice résolu n°2.
Dans la figure ci-dessous, les droites $(AB)$ et $(DE)$ sont parallèles et les droites $(AE)$ et $(BD)$ sont sécantes en $C$.
1°) Calculer les mesures des angles du triangle $ABC$.
2°) Calculer les mesures des angles du triangle $CDE$.

Figure 5.

A terminer.
CQFD $\blacktriangle$