1. Angles adjacents
Définition 12.
Deux angles sont dits adjacents si les trois conditions suivantes sont vérifiées :
1°) Les deux angles ont le même sommet ;
2°) Ils ont un côté commun ;
3°) Et ils sont situés de part et d’autre de ce côté commun.
« de part et d’autre » = « de chaque côté » = « d’un côté et de l’autre côté ». Exemple : « La ville s’étend de part et d’autre du fleuve » = « La ville s’étend d’un côté et de l’autre côté du fleuve ».
Exemples
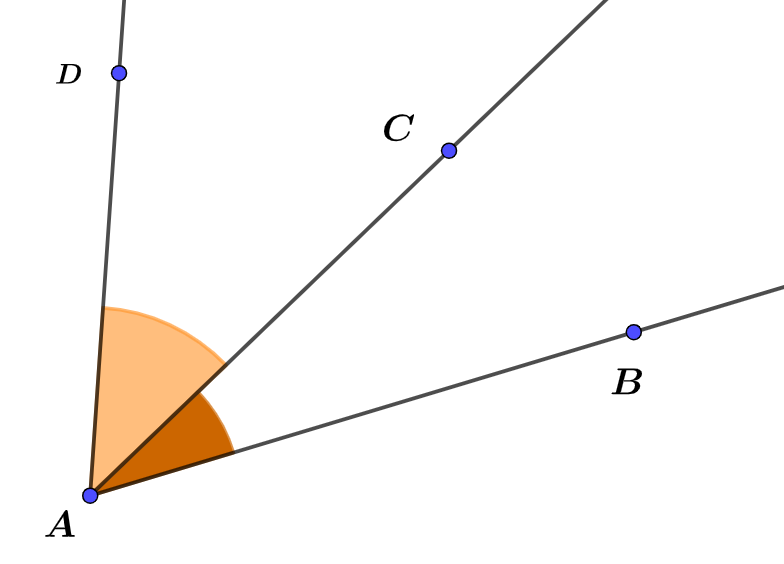
1°) Dans la figure 1, les angles $\widehat{BAC}$ et $\widehat{CAD}$ ont le même sommet $A$, un côté commun $[AC)$ et sont situés de part et d’autre de ce côté commun. Donc les deux angles $\widehat{BAC}$ et $\widehat{CAD}$ sont adjacents.
2°) Dans la figure 1, les angles $\widehat{BAC}$ et $\widehat{BAD}$ ont le même sommet $A$, un côté commun $[AB)$, mais ils ne sont pas situés de part et d’autre de ce côté commun. Donc les deux angles $\widehat{BAC}$ et $\widehat{BAD}$ ne sont pas adjacents.
3°) Dans le figure 2 ci-dessous, les angles $\widehat{BEC}$ et $\widehat{CAD}$ sont-ils adjacents ?
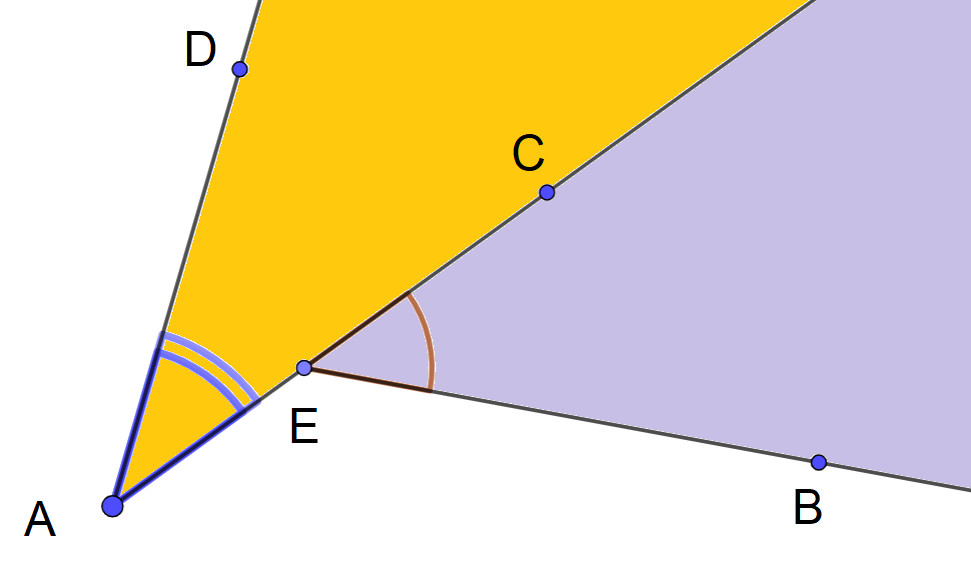
Les deux angles $\widehat{BEC}$ et $\widehat{CAD}$ ne sont pas adjacents car ils n’ont pas le même sommet.
Propriété 1.
Si deux angles $\widehat{BAC}$ et $\widehat{CAD}$ (figure 1.) sont adjacents, alors la mesure de l’angle $\widehat{BAD}$ est égale à la somme des mesures des deux angles $\widehat{BAC}$ et $\widehat{CAD}$ : $$\boxed{~\widehat{BAC}+\widehat{CAD}=\widehat{BAD}~}$$
2. Exercices résolus
Exercice résolu n°1.
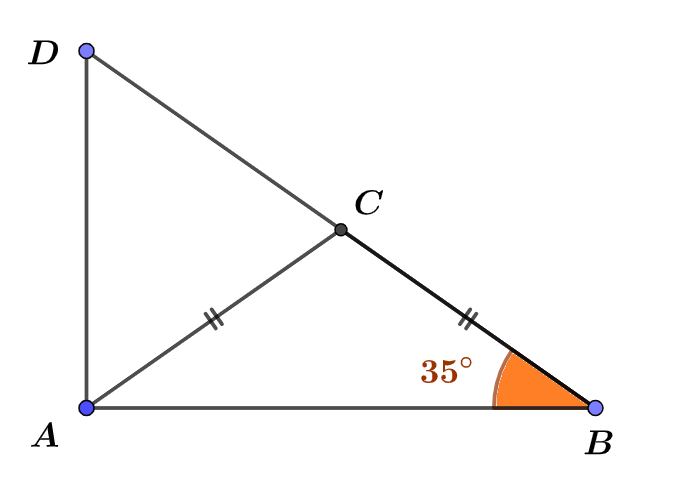
Construire un triangle $ABD$ rectangle en $A$ et tel que $AB=10$ cm et $\widehat{ABD}=35°$.
Placer le point $C$ sur le côté $[AB]$ tel que $ABC$ soit un triangle isocèle en $C$. Toutes les réponses doivent être justifiées.
1°) Faire une figure.
2°) Déterminer la mesure de l’angle : $\widehat{BAC}$.
3°) Calculer la mesure de l’angle : $\widehat{ACB}$.
4°) Calculer la mesure de l’angle : $\widehat{ACD}$.
5°) Calculer la mesure de l’angle : $\widehat{CAD}$.
6°) Calculer la mesure de l’angle : $\widehat{ADB}$.
1°) Construction de la figure :
2°) Déterminer la mesure de l’angle : $\widehat{BAC}$.
D’une part, on sait que, dans le triangle $ABC$ : $\widehat{ABC}=35°$.
D’autre part, le triangle $ABC$ est isocèle en $C$. Donc, ses deux angles à la base sont de même mesure. Donc : $\widehat{BAC}=\widehat{ABC}$.
Par conséquent : $\boxed{~\widehat{BAC}=35^\circ~}$
3°) Calculer la mesure de l’angle : $\widehat{ACB}$.
On sait que, dans le triangle $ABC$ : $\widehat{ABD}=35°$ et $\widehat{ABC}=35°$.
Or, « Dans un triangle quelconque, la somme des mesures des trois angles est égale à 180° ». Donc : $\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180°$
Ce qui donne : $\widehat{ACB}+35°+35°=180°$$
Ou encore : $\widehat{ACB}+70°=180°$
Et par soustraction, on obtient : $\widehat{ACB}=180°-70°$
Conclusion. $\boxed{~\widehat{ACB}=110^\circ~}$
4°) Calculer la mesure de l’angle : $\widehat{ACD}$.
On sait que, les deux angles $\widehat{ACB}$ et $\widehat{ACD}$ sont adjacents et forment un angle plat. Ils sont supplémentaires.
Donc : $\widehat{ACB}+\widehat{ACD}=180°$
Ce qui donne : $110°+\widehat{ACD}=180°$
Et par soustraction, on obtient : $\widehat{ACD}=180°-110°$
Conclusion. $\boxed{~\widehat{ACD}=70^\circ~}$
5°) Calculer la mesure de l’angle : $\widehat{CAD}$.
On sait que, les deux angles $\widehat{CAB}$ et $\widehat{CAD}$ sont adjacents et forment un angle droit. Ils sont complémentaires.
Donc : $\widehat{CAB}+\widehat{CAD}=90°$
Ce qui donne : $35°+\widehat{CAD}=90°$
Et par soustraction, on obtient : $\widehat{CAD}=90°-35°$
Conclusion. $\boxed{~\widehat{CAD}=55^\circ~}$
6°) Calculer la mesure de l’angle : $\widehat{ADB}$.
On sait que, le triangle $ABD$ est rectangle en $A$ et $\widehat{ABD}=35°$.
Or, « Dans un triangle rectangle, les deux angles aigus sont complémentaires »
Donc : $\widehat{ABD}+\widehat{ADB}=90°$
Ce qui donne : $35°+\widehat{ADB}=90°$
Et par soustraction, on obtient : $\widehat{ADB}=90°-35°$
Conclusion. $\boxed{~\widehat{ADB}=55^\circ~}$.